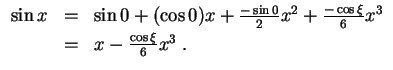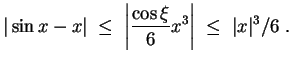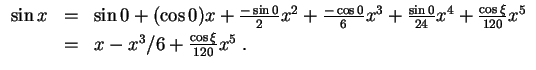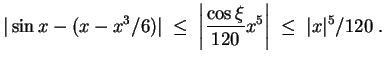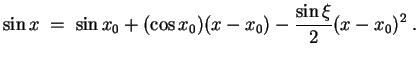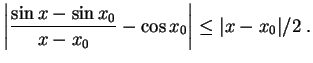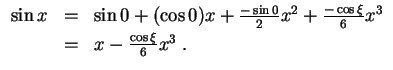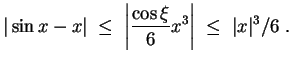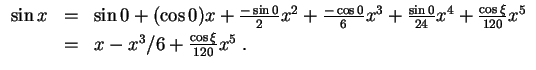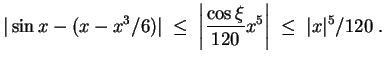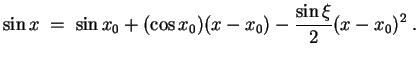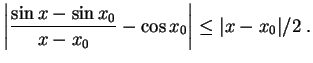- Die Taylorentwicklung des Sinus um
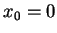 mit
mit
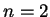 liefert ein
liefert ein
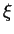 zwischen
zwischen
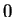 und
und
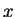 so, daß
Daraus folgt
so, daß
Daraus folgt
- Die Taylorentwicklung des Sinus um
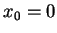 mit
mit
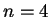 liefert ein
liefert ein
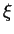 zwischen
zwischen
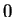 und
und
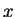 so, daß
Daraus folgt
so, daß
Daraus folgt
- Der Mittelwertsatz liefert ein
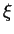 zwischen
zwischen
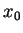 und
und
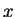 so, daß
Daraus folgt
so, daß
Daraus folgt
- Die Taylorentwicklung des Sinus um
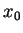 mit
mit
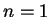 liefert ein
liefert ein
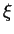 zwischen
zwischen
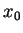 und
und
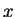 so, daß
Daraus folgt nach Division durch
so, daß
Daraus folgt nach Division durch
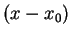 Mit anderen Worten, die Sekantensteigung konvergiert gegen die Tangentensteigung bei
Mit anderen Worten, die Sekantensteigung konvergiert gegen die Tangentensteigung bei
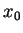 mindestens so schnell wie
mindestens so schnell wie
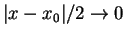 .
.