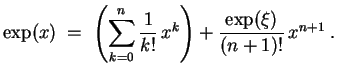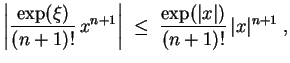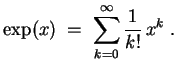Der Satz von Taylor, angewandt auf
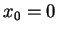 und
und
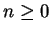 , liefert ein
, liefert ein
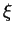 zwischen
zwischen
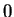 und
und
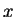 mit
mit
Wegen
und wegen
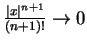 für
für
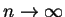 , konvergiert die Partialsumme
, konvergiert die Partialsumme
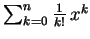 gegen
gegen
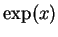 , d.h.
Hierbei folgt
, d.h.
Hierbei folgt
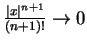 für
für
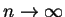 aus der (z.B. nach dem Quotientenkriterium)
bekannten Konvergenz eben jener Reihe
aus der (z.B. nach dem Quotientenkriterium)
bekannten Konvergenz eben jener Reihe
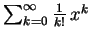 für
für
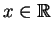 , und
aus der notwendigen Bedingung für Reihenkonvergenz, daß die zu summierende Folge gegen Null strebt.
, und
aus der notwendigen Bedingung für Reihenkonvergenz, daß die zu summierende Folge gegen Null strebt.
![]() und
und
![]() , liefert ein
, liefert ein
![]() zwischen
zwischen
![]() und
und
![]() mit
mit