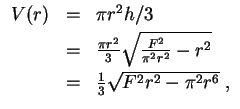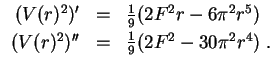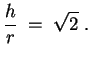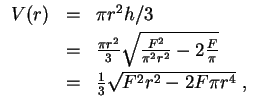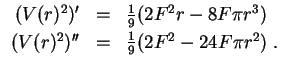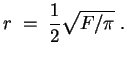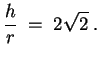Das zu maximierende Volumen beträgt
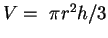 , mit dem Grundkreisradius
, mit dem Grundkreisradius
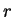 und der Höhe
und der Höhe
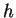 .
.
- (1)
- Mit
wobei
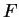 die Oberfläche ohne Grundkreis bezeichnet, werden
Damit erhalten wir für
die Oberfläche ohne Grundkreis bezeichnet, werden
Damit erhalten wir für
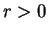 einen Extremstellenkandidaten von
einen Extremstellenkandidaten von
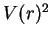 (und damit auch von
(und damit auch von
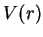 ) bei
Es ist dort
) bei
Es ist dort
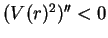 , also liegt ein Maximum vor. Die Höhe des Maximalkegels ergibt sich zu
und wir erhalten
, also liegt ein Maximum vor. Die Höhe des Maximalkegels ergibt sich zu
und wir erhalten
- (2)
- Mit
wobei
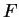 die Oberfläche bezeichnet, werden
Damit erhalten wir für
die Oberfläche bezeichnet, werden
Damit erhalten wir für
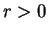 einen Extremstellenkandidaten von
einen Extremstellenkandidaten von
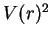 (und damit auch von
(und damit auch von
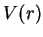 ) bei
Es ist dort
) bei
Es ist dort
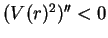 , also liegt ein Maximum vor. Die Höhe des Maximalkegels ergibt sich zu
und wir erhalten
, also liegt ein Maximum vor. Die Höhe des Maximalkegels ergibt sich zu
und wir erhalten
![]() , mit dem Grundkreisradius
, mit dem Grundkreisradius
![]() und der Höhe
und der Höhe
![]() .
.