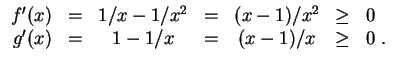
![$ \mbox{$\displaystyle
\begin{array}{rcl}
f'(x) &=& \alpha(1+x)^{\alpha-1}-\alp...
...}$} und {$\mbox{$\alpha\in[0,1]$}$}}}\\
\end{array}\right. \;.
\end{array}$}$](img12.gif)
Falls
![]() , ist
, ist
![]() nach dem Monotoniekriterium monoton wachsend auf
nach dem Monotoniekriterium monoton wachsend auf
![]() und monoton fallend
auf
und monoton fallend
auf
![]() . Da
. Da
![]() , folgt
, folgt
![]() für
für
![]() .
.
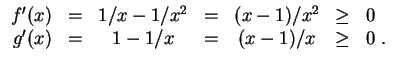
![$ \mbox{$\displaystyle
\begin{array}{rcl}
f'(x) &=& \alpha(1+x)^{\alpha-1}-\alp...
...}$} und {$\mbox{$\alpha\in[0,1]$}$}}}\\
\end{array}\right. \;.
\end{array}$}$](img12.gif)
Falls
![]() , ist
, ist
![]() nach dem Monotoniekriterium monoton wachsend auf
nach dem Monotoniekriterium monoton wachsend auf
![]() und monoton fallend
auf
und monoton fallend
auf
![]() . Da
. Da
![]() , folgt
, folgt
![]() für
für
![]() .
.