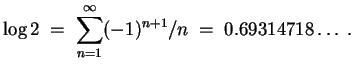Lösung.

Es wird mit der geometrischen Reihe für $ \mbox{$\vert x-1\vert<1$}$

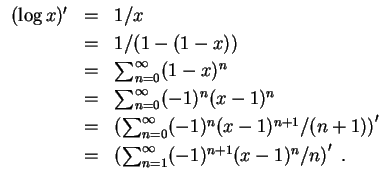
$ \mbox{$\displaystyle \begin{array}{rcl} (\log x)' &=& 1/x \vspace*{1mm}\\ &... ... &=& \left(\sum_{n=1}^\infty (-1)^{n+1} (x-1)^n/n\right)'\; .\\ \end{array}$}$

Somit ist

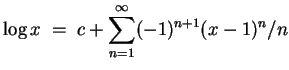
$ \mbox{$\displaystyle \log x\;=\; c+\sum_{n=1}^\infty (-1)^{n+1} (x-1)^n/n $}$
mit einer Konstanten $ \mbox{$c\in\mathbb{R}$}$. Durch Einsetzen von $ \mbox{$x=1$}$ erhalten wir $ \mbox{$c=0$}$ und
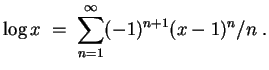
$ \mbox{$\displaystyle \log x\;=\; \sum_{n=1}^\infty (-1)^{n+1} (x-1)^n/n \; . $}$

Die so erhaltene Potenzreihe hat den Konvergenzradius

$ \mbox{$\displaystyle R\;=\; \frac{1}{\overline {\lim}_{n\to\infty}\sqrt[n]{\vert(-1)^{n+1}/n\vert}} \;=\; 1 \;. $}$
Alternativ kann man den Konvergenzradius $ \mbox{$1$}$ der geometrischen Reihe verwenden und die Tatsache, daß sich beim Ableiten einer Potenzreihe der Konvergenzradius nicht ändert.

Folglich konvergiert die Potenzreihe für $ \mbox{$x\in (0,2)$}$ und divergiert für $ \mbox{$x\in (-\infty,0)\cup(2,\infty)$}$. Für $ \mbox{$x=0$}$ divergiert sie als harmonische Reihe. Für $ \mbox{$x=2$}$ konvergiert sie mit dem Leibnizkriterium.

Insbesondere haben wir

$ \mbox{$\displaystyle \log 2 \;=\; \sum_{n=1}^\infty (-1)^{n+1}/n \;=\; 0.69314718\ldots \;. $}$