
 und wo ist der Meistereder?
und wo ist der Meistereder?Auf dieser Seite findet man Bilder der fünf regulären Polyeder (Tetraeder, Würfel=Hexaeder, Oktaeder, Dodekaeder, Ikosaeder) sowie Bastelbogen, mit denen man sich Modelle zur Stärkung der Abschauung fertigen kann.
Insbesondere gibt es einen Bastelbogen, mit dem man einen Fußball als Schnittfigur von Dodekaeder und Ikosaeder herstellen kann (der hier erzeugte Fußball ist die klassische Variante mit einfacher Drehgruppe der Ordnung 60, nicht so ein neumodischer mit viel kleinerer und dann auflösbarer Symmetriegruppe).
Schließlich kann man sich auch noch mathematisch bilden, indem man eine Abhandlung über die Konstruktion des Ikosaeders liest...
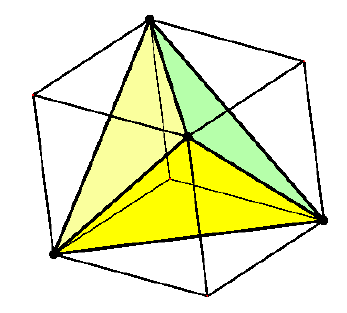
Das Tetraeder, in einen Würfel einbeschrieben
 |
Das Oktaeder als Dual des Hexaeders
 |
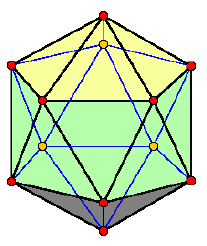
Das Ikosaeder
 |
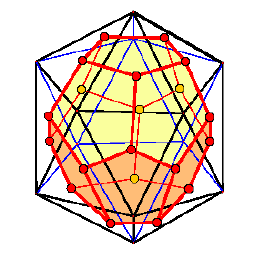
Das Dodekaeder als Dual des Ikosaeders
 |
 und wo ist der Meistereder?
und wo ist der Meistereder? |
Ein Fußball entsteht durch Abstumpfen (Kappen der Ecken)
wahlweise aus einem Dodekaeder oder einem Ikosaeder.
Ein schönes Modell können Sie aus diesem Bastelbogen
gewinnen:
als
PDF-Datei.
Sie müssen die gefärbte Fläche ausschneiden, dabei
entlang der dickeren Linien in die Innengebiete schneiden. Danach
werden von den sechs Sechsecken, die ein sechseckiges Loch umgeben,
jeweils die an die Schnittlinie angrenzenden auf einander geklebt: So
entstehen fünfeckige Löcher.
"Es ist sehr leicht (etwa durch Angabe in Koordinaten),
reguläre Körper anzugeben, bei denen die
Anzahl der Seitenflächen einen der Werte 4
(so genannte Tetraeder),
6 (Typ (4,3): Hexaeder bzw. Würfel) oder
8 (Typ (3,4): Oktaeder) annimmt.
Im Folgenden sollen - mit Hilfe elementarer Gruppentheorie -
reguläre Körper konstruiert werden, bei denen Anzahl
der Seitenflächen
12 (Typ (5,3): Dodekaeder) oder
20 (Typ (3,5): Ikosaeder) beträgt.
...
Ziel dieser
Notizen ist es, erste Erfahrungen und Kenntnisse über Gruppen und
Gruppenwirkungen anzuwenden und damit einzuüben. "
Sie können eine PDF-Datei laden.