
Wir sehen (mit den nötigen Zugeständnissen) die Oberfläche des Freigeländes als Graph einer Funktion in zwei Veränderlichen an.
Die hier angebotenen Fotos sind vom Autor gemachte Originalaufnahmen oder Bearbeitungen von solchen. Die Grafiken wurden vom Autor erzeugt mit Maple.
Auf dem Campus finden sich
– und außerdem einige Kunstwerke mit mathematischem oder physikalischem Gehalt.
Lokale Maxima |

|

|
Die betonierten Halbkugeln liefern offensichtlich lokale Maxima. In grober Näherung (und bei geeignet gewähltem Maßstab) können wir das Gelände in einer Umgebung einer solchen Halbkugel durch die folgende Funktion beschreiben: \[ f \colon \mathbb{R}^2 \to \mathbb{R} \colon \left(x\atop y\right) \mapsto \sqrt{\max\{4-x^2-y^2,0\}} \] Diese Funktion ist stetig, und sie ist partiell differenzierbar an allen Stellen in \( \mathbb{R}^2 \) außer denen, die auf dem Kreis \( \left\{ \left(\left. x\atop y\right) \,\right|\, x^2+y^2=4 \right\} \) liegen.
Wer jetzt lieber rechnen statt fühlen will, bitte sehr:
An den Stellen im Innern dieses Kreises ergibt sich der Gradient dann als
\[
\nabla f\left(x\atop
y\right) = \frac{-1}{\sqrt{4-x^2-y^2}}\left(x\atop y\right)
\]
und wird offenbar genau dann zum Nullvektor, wenn
\(
\left(x\atop y\right) = \left(0\atop 0\right)
\).
Dass dort ein (lokales) Maximum vorliegt, sehen wir unmittelbar; wir
können das aber auch daran ablesen, dass die Hesse-Matrix
\[
\mathrm{H}f \left(x\atop y\right) =
\frac1{\left(\sqrt{4-x^2-y^2}\right)^3}\pmatrix{y^2-4&-xy\\-xy&y^2-4}
\]
an der Stelle \(\left(0\atop0\right)\) zu
\(
\mathrm{H}f\left(0\atop0\right) = \frac12\left({-1\atop0}\,{0\atop-1}\right)
\)
und damit offensichtlich negativ definit wird.
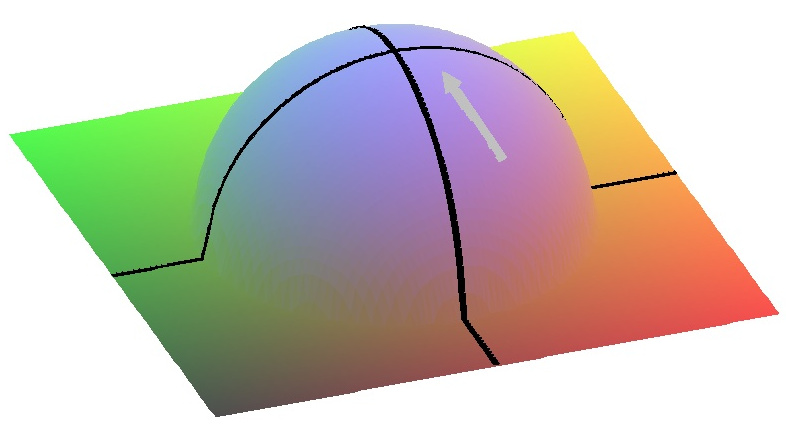
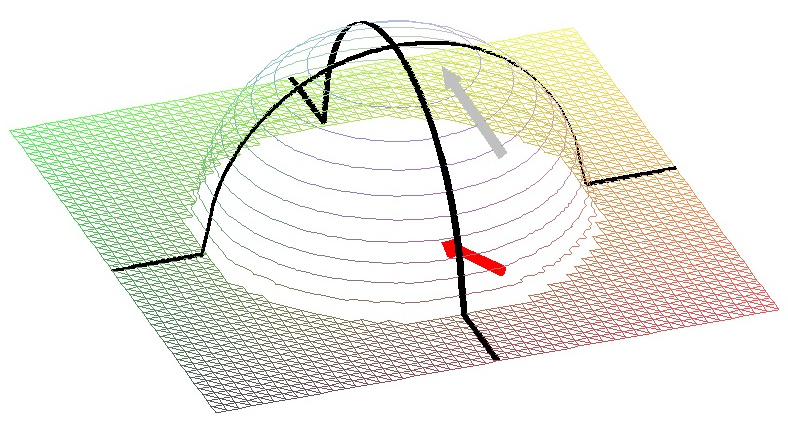
Auf dem Beton ist durch eine Kreidemarkierung ein Tangentialvektor angedeutet, der in Richtung des steilsten Anstiegs der Fläche verläuft. Wenn man diesen (an den Punkt \(\left(a,b,f(a,b)\right)^\intercal\) angesetzten) Tangentialvektor orthogonal nach unten projiziert (in den "Grundriss"), erhält man den Gradienten der Funktion \(f\) im Punkt \(\left(a\atop b\right)\). In der rechten Grafik sieht man den Gradienten als roten Pfeil in der Grundebene.
|
|
Rechnerisch kann man diesen Tangentialvektor so ermitteln: Der Gradient \(\nabla f\left(a\atop b\right)\) wird an der Stelle \(\left(a,b,f(a,b)\right)^\intercal\) angesetzt. Damit erhalten wir die Grundseite eines Steigungsdreiecks (in der Skizze rechts hellblau angedeutet) für die fragliche Tangente. Die Steigung dieser Tangente ergibt sich aus der Richtungsableitung: Wir normieren \( v:= \frac1{|\nabla f\left(a\atop b\right)|} \nabla f\left(a\atop b\right) \) \[ \partial_v f\left(a\atop b\right) = v\bullet\nabla f\left(a\atop b\right) = \frac{\nabla f\left(a\atop b\right)\bullet\nabla f\left(a\atop b\right)} {\sqrt{\nabla f\left(a\atop b\right)\bullet\nabla f\left(a\atop b\right)}} = \sqrt{\nabla f\left(a\atop b\right)\bullet\nabla f\left(a\atop b\right)} = \left|\nabla f\left(a\atop b\right)\right| = \sqrt{\frac{x^2+y^2}{4-x^2-y^2}} . \]
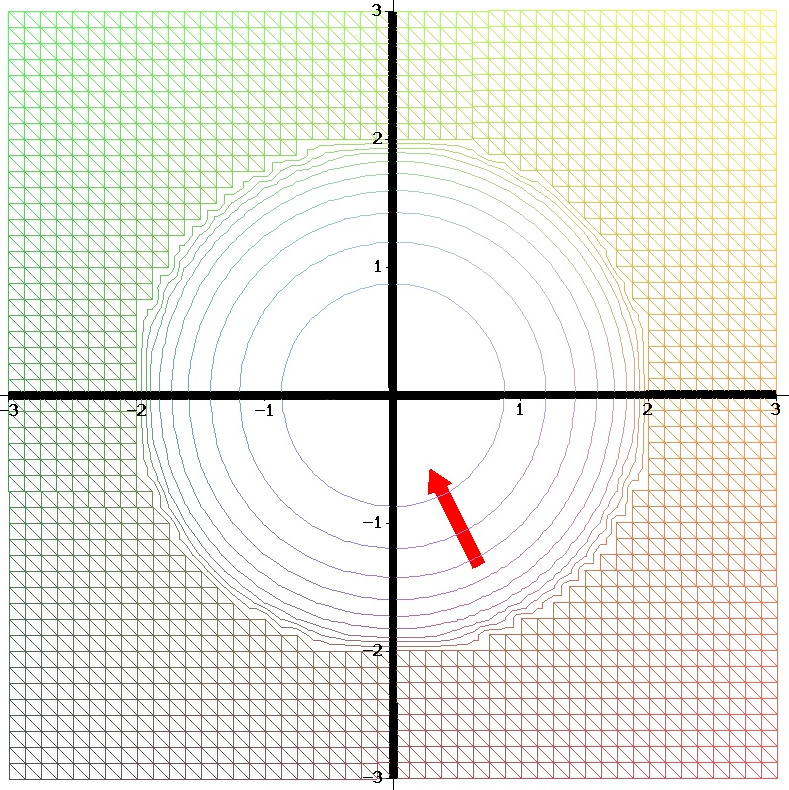
Speziell an der Stelle \(\left(a\atop b\right) = \left(1/3\atop-2/3\right)\), die in etwa der Kreidemarkierung entspricht, erhalten wir den Gradienten \( \nabla f\left(1/3\atop-2/3\right) = \frac1{\sqrt{31}}\left(-1\atop2\right) \) und damit die Steigung \(3\sqrt{5/31} \approx 1,2\).
|
|
Lokale Minima |
Ein lokales Minimum (und das ist gut so),
gekennzeichnet durch das Symbol
 :
:

An der hier wieder durch das Symbol
 gekennzeichneten Stelle hätte man sich ebenfalls ein lokales Minimium
erhofft - leider ging das schief.
gekennzeichneten Stelle hätte man sich ebenfalls ein lokales Minimium
erhofft - leider ging das schief.
Die farbliche Hervorhebung im rechten Bild deutet einen (durch die
Wasseroberfläche eingenommenen) Teil einer Niveaumenge an.

|

|
| inzwischen wurde ein Reparaturversuch unternommen: |

|
Sattelpunkte |
Auch Sattelpunkte kann man (nach etwas intensiverer Suche) auf dem Campus entdecken (rechts im größeren Kontext, damit man das leichter wiederfindet):

|

|
Eine Funktion, deren Graph wenigsten einigermaßen dem Kunstwerk ähnelt, ist die folgende: \[ h \colon (0,4)\times(-2,2) \to \mathbb{R} \colon \left(x\atop y\right) \mapsto \sqrt{\max\left\{ \textstyle\left(\frac1{12}\,x^3-\frac12\,x^2+\frac34\,x+\frac13\right)^2-y^2 ,0 \right\}} \]
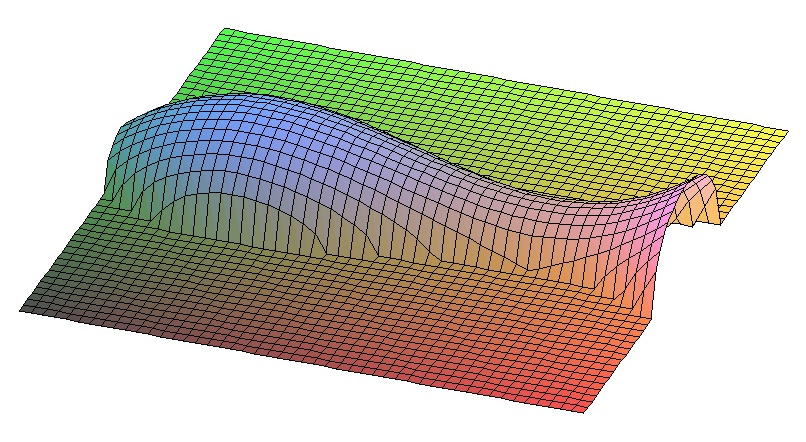
Der Gradient von \(h\) erscheint einigermaßen widerlich: \[ \nabla h \left(x\atop y\right) = \frac1{\sqrt{x^6-12\,x^5+54\,x^4-102\,x^3+45\,x^2-36\,y^2+54\,x+9}} \left(\frac1{12}(6\,x^5-60\,x^4+216\,x^3-306\,x^2+90\,x+54)\atop {-6\,y}\right) \] - aber der Nenner ist uns bei der Suche nach Nullstellen des Gradienten zum Glück egal, und für die erste Komponente des Zählers finden wir die Nullstellen \(1\) und \(3\). Polynomdivision liefert dann: \[ 6\,x^5-60\,x^4+216\,x^3-306\,x^2+90\,x+54 = (x^3-6\,x^2+9\,x+3)(x-3)(x-1) \,. \] Im Definitionsbereich läuft \( x \) nur zwischen \(0\) und \(4\); dort hat der Faktor \( x^3-6\,x^2+9\,x+3 \) keine Nullstellen. Es ergeben sich also zwei kritische Stellen, nämlich \( \left(1\atop 0\right) \) und \( \left(3\atop 0\right) \). Unser Sattelpunkt liegt bei \( \left(3\atop 0\right) \).
Die Hesse-Matrix ersparen wir uns lieber ... hier sieht man noch die beiden waagrechten Tangentialebenen:
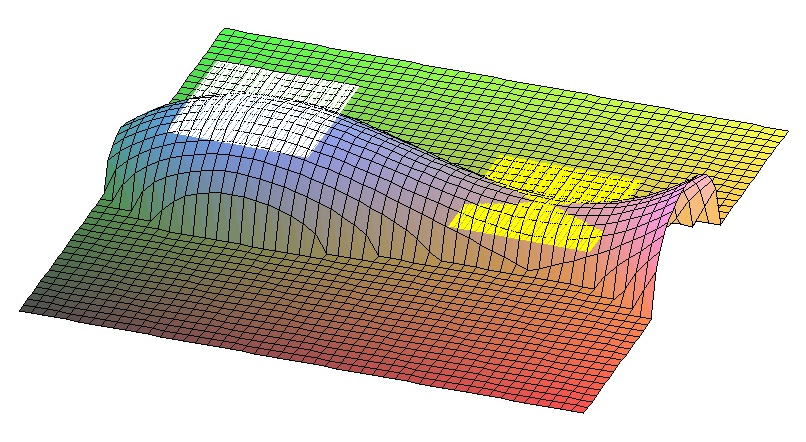
Sattelpunkte, die wirklich so aussehen wie unsere Maple-Grafiken, findet man auf dem Campus auch:

Mehr Sattelpunkte auf dem Campus kamen bei einem Wettbewerb Ende des Sommersemesters 2014 zu Tage.
| IMPRESSUM. | OPPOSSUM. |