Recurrence Relations for Multivariate B-Splines

For a convex polyhedron $ Q\subset\mathbb{R}^m$ and a linear map $ P$ of $ \mathbb{R}^m$ onto $ \mathbb{R}^n$,

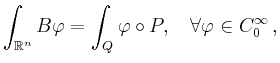
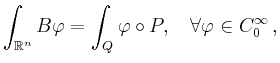
$\displaystyle \int_{\mathbb{R}^n} B\varphi = \int_Q \varphi\circ P,\quad \forall \varphi\in C^\infty_0 \,, $

defines a multivariate b-spline $ B$.

\includegraphics[width=12cm,clip]{RecurrenceFig.eps}

If $ B_k$ denotes the b-splines corresponding to the faces $ Q_k$ of $ Q$,

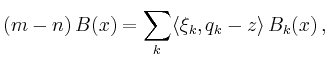
$\displaystyle (m-n)\,B(x) = \sum_k \langle \xi_k,q_k-z\rangle\,B_k(x) \,, $

for all points $ x=Pz$ where $ B$ and $ B_k$ are continuous and with $ \xi_k$ the normal to $ Q_k$ and $ q_k\in Q_k$.

This general formula implies the recurrence relations for box- and simplex-splines as special cases.


$ \square$ with C. de Boor, Proc. Amer. Math. Soc. 85 (1982), 397-400.

[previous] [next]