Eine Laplacetransformation nach
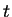 ergibt mit
ergibt mit
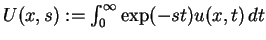 die transformierte Gleichung
die transformierte Gleichung
Die zugehörige homogene Gleichung wird von
 gelöst. Eine Partikulärlösung der inhomogenen Gleichung ist durch
gelöst. Eine Partikulärlösung der inhomogenen Gleichung ist durch
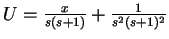 gegeben, wie man direkt oder mittels Variation der Konstanten erhält. Somit wird die allgemeine Lösung zu
wobei
gegeben, wie man direkt oder mittels Variation der Konstanten erhält. Somit wird die allgemeine Lösung zu
wobei
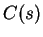 eine von
eine von
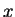 unabhängige Funktion bezeichne (die man durch die Randbedingungen für die Rücktransformierte bestimmen könnte).
unabhängige Funktion bezeichne (die man durch die Randbedingungen für die Rücktransformierte bestimmen könnte).
Für
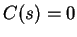 erhalten wir
erhalten wir
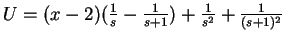 , und folglich
, und folglich
Nun ist in der Tat
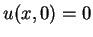 und
und
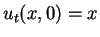 . Die Ausgangsdifferentialgleichung ist nach Konstruktion erfüllt. Nichtsdestoweniger empfiehlt sich eine Probe.
. Die Ausgangsdifferentialgleichung ist nach Konstruktion erfüllt. Nichtsdestoweniger empfiehlt sich eine Probe.
![]() ergibt mit
ergibt mit
![]() die transformierte Gleichung
die transformierte Gleichung
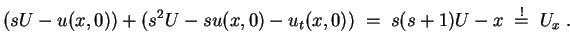
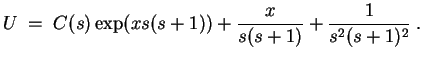
![]() erhalten wir
erhalten wir
![]() , und folglich
, und folglich