Es ist
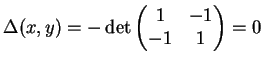 für alle
für alle
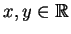 , die Gleichung auf
, die Gleichung auf
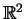 also parabolisch.
Als Lösung von
also parabolisch.
Als Lösung von
erkennen wir
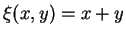 , wobei in der Tat
, wobei in der Tat
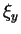 nicht identisch verschwindet. Sei
nicht identisch verschwindet. Sei
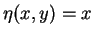 .
Variablensubstitution ergibt
Durch zweimalige Integration erhält man schließlich
mit beliebigen (zweimal differenzierbaren) Funktionen
.
Variablensubstitution ergibt
Durch zweimalige Integration erhält man schließlich
mit beliebigen (zweimal differenzierbaren) Funktionen
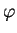 und
und
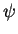 . Eine Probe empfiehlt sich.
. Eine Probe empfiehlt sich.
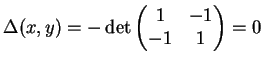 für alle
für alle
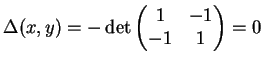 für alle
für alle
![]() , die Gleichung auf
, die Gleichung auf
![]() also parabolisch.
Als Lösung von
also parabolisch.
Als Lösung von