Es ist
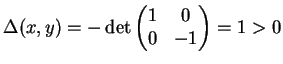 für alle
für alle
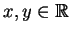 , die Gleichung also auf
, die Gleichung also auf
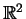 hyperbolisch.
Als Lösungen von
hyperbolisch.
Als Lösungen von
sind
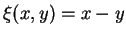 resp.
resp.
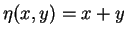 ersichtlich.
Variablensubstitution ergibt für die ursprüngliche Gleichung
Setzt man
ersichtlich.
Variablensubstitution ergibt für die ursprüngliche Gleichung
Setzt man
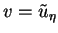 , so wird
, so wird
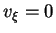 durch
durch
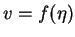 mit einer
beliebigen Funktion
mit einer
beliebigen Funktion
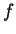 gelöst. Integration von
gelöst. Integration von
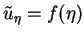 ergibt
schließlich
mit beliebigen (zweimal differenzierbaren) Funktionen
ergibt
schließlich
mit beliebigen (zweimal differenzierbaren) Funktionen
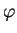 und
und
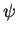 .
.
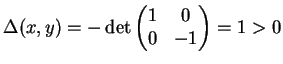 für alle
für alle
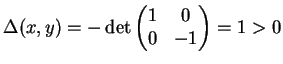 für alle
für alle
![]() , die Gleichung also auf
, die Gleichung also auf
![]() hyperbolisch.
Als Lösungen von
hyperbolisch.
Als Lösungen von