Lösung.

Fall (i). Zu lösen ist $ \mbox{$u_t - u_x = 0$}$. Als System für die Höhenlinien erhalten wir für einen freien Parameter $ \mbox{$s$}$ das System

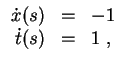
$ \mbox{$\displaystyle \begin{array}{rcl} \dot x(s) & = & -1 \\ \dot t(s) & = & 1\; , \\ \end{array}$}$
woraus wir $ \mbox{$\frac{dx}{dt} = -1$}$ entnehmen. Als Lösung ergibt sich $ \mbox{$x + t = {\mbox{const.}}$}$, so daß die ursprüngliche Gleichung die allgemeine Lösung $ \mbox{$v(x + t)$}$ besitzt.

Fall (ii). Zu lösen ist zunächst die Rumpfdifferentialgleichung $ \mbox{$u_t - (1+a\cos(x)) u_x = 0$}$. Als System für die Höhenlinien erhalten wir für einen freien Parameter $ \mbox{$s$}$ das System

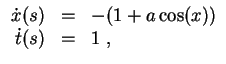
$ \mbox{$\displaystyle \begin{array}{rcl} \dot x(s) & = & -(1+a\cos(x)) \\ \dot t(s) & = & 1\; , \\ \end{array}$}$
woraus wir $ \mbox{$\frac{dx}{dt} = -(1+a\cos(x))$}$ entnehmen, d.h. $ \mbox{$\int dt = - \int (1 + a\cos(x))^{-1} dx$}$. Es wird
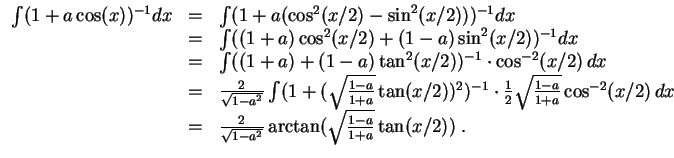
$ \mbox{$\displaystyle \begin{array}{rcl} \int (1 + a\cos(x))^{-1} dx & = & \in... ...{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2))\; . \\ \end{array}$}$

Als Lösung ergibt sich 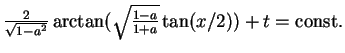$ \mbox{$\frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2)) + t = {\mbox{const.}}$}$, so daß die Rumpfgleichung die allgemeine Lösung 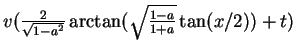$ \mbox{$v(\frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2)) + t)$}$ besitzt. Für $ \mbox{$a = 0$}$ ergibt sich also tatsächlich die Lösung aus (i) (dort lag ja schon eine Rumpfdifferentialgleichung vor).

Für die Lösung der ursprünglichen Gleichung können wir etwa die Transformation

$ \mbox{$\displaystyle \begin{array}{rcl} \xi & = & x \\ \tau & = & t + \frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2))\; , \\ \end{array}$}$
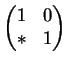verwenden, was wegen Jacobimatrix $ \mbox{$\left(\begin{matrix}1 & 0 \\ \ast & 1\end{matrix}\right)$}$ zulässig ist. Es bleibt
$ \mbox{$\displaystyle -(1 + a\cos(\xi)) \tilde u_\xi + a\sin(\xi)\tilde u \; =\; 0\; . $}$
zu lösen. Es ergibt sich zunächst
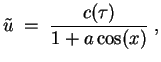
$ \mbox{$\displaystyle \tilde u \; =\; \frac{c(\tau)}{1 + a\cos(x)}\; , $}$
und rücksubstituiert also
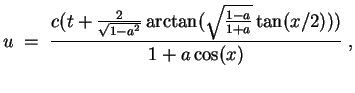
$ \mbox{$\displaystyle u \; =\; \frac{c(t + \frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2)))}{1 + a\cos(x)}\; , $}$
mit einer beliebigen Funktion $ \mbox{$c$}$.

Nun ist noch das Anfangswertproblem zu lösen.

Im Fall (i) ergibt sich mit $ \mbox{$u(x,0) = v(x) = 1/2$}$, daß $ \mbox{$v$}$ konstant gleich $ \mbox{$1/2$}$ ist, und somit $ \mbox{$u(x,t) = 1/2$}$ gilt. Der Verkehr fließt störungsfrei.

Im Fall (ii) ergibt die Randbedingung

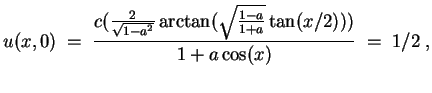
$ \mbox{$\displaystyle u(x,0) \; =\; \frac{c(\frac{2}{\sqrt{1 - a^2}}\arctan(\sqrt{\frac{1-a}{1+a}}\tan(x/2)))}{1 + a\cos(x)} \; =\; 1/2\; , $}$
daß im Ausdruck für $ \mbox{$u(x,t)$}$ auftretende Funktion $ \mbox{$c = c(w)$}$ gegeben ist durch
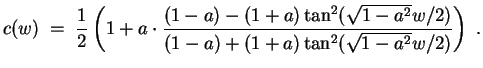
$ \mbox{$\displaystyle c(w)\; =\; \frac{1}{2}\left(1 + a \cdot \frac{(1-a) - (1... ...(\sqrt{1 - a^2} w/2)}{(1-a) + (1 + a)\tan^2(\sqrt{1 - a^2} w/2)}\right) \; . $}$
Hierbei ist $ \mbox{$w$}$ eine Hilfsvariable. Graphisch verläuft für $ \mbox{$a = 0.5$}$ die Verkehrsdichte $ \mbox{$u$}$ in Abhängigkeit von Zeit $ \mbox{$t$}$ und Ort $ \mbox{$x$}$ wie folgt.

\includegraphics [width=10cm]{s2.eps}

Eine gleichmäßige Verkehrsdichte wird gestört.