Lösung.

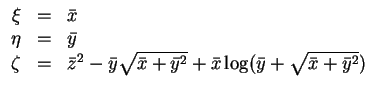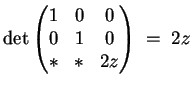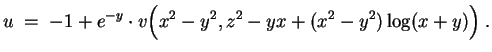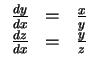
Als System für das Höhengebilde erhalten wir

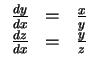
$ \mbox{$\displaystyle \begin{array}{rcl} \frac{dy}{dx} & = & \frac{x}{y} \\ \frac{dz}{dx} & = & \frac{y}{z} \\ \end{array}$}$
Es sind keine $ \mbox{$2$}$ unabhängigen Lösungen ersichtlich (bei normaler Wahrnehmung).

Unter der Zusatzvoraussetzung $ \mbox{$u_z = 0$}$ reduziert sich dieses System aber zu $ \mbox{$\frac{dy}{dx} = \frac{x}{y}$}$, und wir erhalten als Charakteristik dieses Systems $ \mbox{$x^2 - y^2 = {\mbox{const}}$}$, also als Partikulärlösung $ \mbox{$u = x^2 - y^2$}$. Diese ist in der Tat nicht von $ \mbox{$z$}$ abhängig, und stellt somit eine Partikulärlösung der ursprünglichen Rumpfgleichung dar. Nun ist aber $ \mbox{$1 < 2 = n-1$}$, d.h. wir haben bislang eine Lösung zu wenig.

Wir führen eine Koordinatentransformation durch. Sei

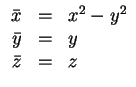
$ \mbox{$\displaystyle \begin{array}{rcl} \bar x & = & x^2 - y^2 \\ \bar y & = & y \\ \bar z & = & z \\ \end{array}$}$
Hierbei ist Sorge zu tragen, daß die Jacobideterminante
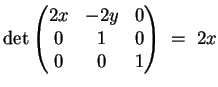
$ \mbox{$\displaystyle \det\left(\begin{matrix}2x & -2y & 0 \\ 0 & 1 & 0\\ 0 & 0 & 1\end{matrix}\right) \; =\; 2x $}$
nicht identisch verschwindet. Die Umkehrtransformation lautet
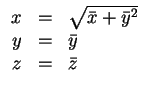
$ \mbox{$\displaystyle \begin{array}{rcl} x & = & \sqrt{\bar x + \bar y^2}\\ y & = & \bar y \\ z & = & \bar z \\ \end{array}$}$
in einem dafür geeigneten Gebiet, i.e. unter Vernachlässigung von Vorzeichenproblemen. Hier sei etwa $ \mbox{$x > 0$}$.

Der Ansatz $ \mbox{$u(x,y,z) = \bar u(\bar x(x,y),\bar y(y),\bar z(z))$}$ ergibt mit der Kettenregel

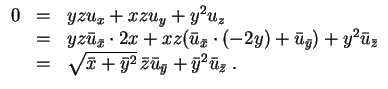
$ \mbox{$\displaystyle \begin{array}{rcl} 0 & = & yz u_x + xz u_y + y^2 u_z \\... ...y^2}\, \bar z \bar u_{\bar y} + \bar y^2 \bar u_{\bar z}\; . \\ \end{array}$}$

Das System für die Charakteristiken ist gegeben durch die eine Gleichung

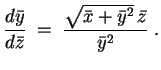
$ \mbox{$\displaystyle \frac{d\bar y}{d\bar z}\; =\; \frac{\sqrt{\bar x + \bar y^2}\, \bar z}{\bar y^2}\; . $}$
Trennung der Variablen liefert
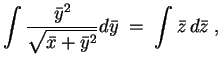
$ \mbox{$\displaystyle \int{\frac{\bar y^2}{\sqrt{\bar x + \bar y^2}} d\bar y}\; =\; \int\bar z\, d\bar z\; , $}$
und also
$ \mbox{$\displaystyle \bar z^2 - \bar y \sqrt{\bar x + \bar y^2} + \bar x \log(y + \sqrt{\bar x + \bar y^2})\; =\; {\mbox{const.}}. $}$
Als weitere Lösung ergibt sich mithin
$ \mbox{$\displaystyle u \; =\; \bar u (\bar x,\bar y,\bar z)\; =\; z^2 - yx + (x^2 - y^2) \log(x + y)\; . $}$
Man prüft nach, daß die Bedingung $ \mbox{$x > 0$}$ wieder entfallen darf. Dafür sollte aber $ \mbox{$x + y > 0$}$ sein.

Nun zur ursprünglichen inhomogenen Gleichung. Wir transformieren zunächst die Koordinaten $ \mbox{$(x,y,z)$}$ wie oben in $ \mbox{$(\bar x,\bar y,\bar z)$}$ und erhalten

$ \mbox{$\displaystyle xz \bar u_{\bar y} + \bar y^2\bar u_{\bar z} + xz\bar u + xz \; =\; 0 \; , $}$
wobei es sich als geschickt erweisen wird, die Transformation teilweise zunächst nicht auszuschreiben.

Wir transformieren nun

$ \mbox{$\displaystyle \begin{array}{rcl} \xi & = & \bar x \\ \eta & = & \bar... ... + \bar y^2} + \bar x\log(\bar y + \sqrt{\bar x + \bar y^2}) \\ \end{array}$}$
Dies ist wegen der nicht identisch verschwindenden Jacobideterminante
$ \mbox{$\displaystyle \det\left(\begin{matrix}1 & 0 & 0 \\ 0 & 1 & 0\\ \ast & \ast & 2z\end{matrix}\right) \; =\; 2z $}$
zulässig. Da $ \mbox{$\zeta$}$ nun eine Lösung der Rumpfgleichung ist, bleibt uns
$ \mbox{$\displaystyle xz\tilde u_{\eta} + xz(\tilde u + 1) \; =\; 0 $}$
zu lösen, wobei $ \mbox{$\bar{u}(\bar{x},\bar{y},\bar{z}) = \tilde{u}(\xi(\bar{x}),\eta(\bar{y}), \zeta( \bar{x},\bar{y},\bar{z}))$}$ ist. Wir erhalten
$ \mbox{$\displaystyle \tilde u \; =\; -1 + e^{-\eta}\cdot c(\xi,\zeta)\; . $}$
Rücktransformiert hat die allgemeine Lösung die Gestalt
$ \mbox{$\displaystyle u \; =\; -1 + e^{-y}\cdot v\Big(x^2 - y^2, z^2 - yx + (x^2 - y^2) \log(x + y)\Big) \; . $}$