Lösung.

Es sind $ \mbox{$F(x, y, y') = F(y, y') = y \sqrt{1+(y')^2}$}$ und $ \mbox{$G(x, y, y') = G(y, y') = \sqrt{1+(y')^2}$}$ nicht explizit von $ \mbox{$x$}$ abhängig. Die integrierte Euler-Lagrange-Differentialgleichung für $ \mbox{$L(y, y') = F(y, y') - \lambda G(y, y')$}$ mit noch zu bestimmendem Lagrange-Multiplikator $ \mbox{$\lambda\in\mathbb{R}$}$ ist für ein konstantes $ \mbox{$c\in\mathbb{R}$}$

$ \mbox{$\displaystyle L(y,y') - y' L_{y'}(y,y') \; =\; c\; . $}$
Eingesetzt erhält man
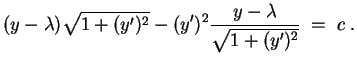
$ \mbox{$\displaystyle (y-\lambda) \sqrt{1+(y')^2} - (y')^2 \frac{y -\lambda}{\sqrt{1+(y')^2}} \; =\; c\; . $}$
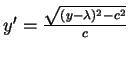Daraus wird durch Umformung $ \mbox{$y' = \frac{\sqrt{ (y-\lambda)^2 - c^2 }}{c}$}$. Diese Differentialgleichung mit getrennten Veränderlichen kann durch Auflösen von
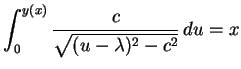
$ \mbox{$\displaystyle \int_0^{y(x)} \frac{c}{\sqrt{(u-\lambda)^2-c^2}}\,du = x $}$
nach $ \mbox{$y(x)$}$ gelöst werden. Mit $ \mbox{$a\in\mathbb{R}$}$ gilt
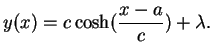
$ \mbox{$\displaystyle y(x) = c \cosh(\frac{x-a}{c}) + \lambda. $}$

Die Rand- und Nebenbedingungen liefern die zur Bestimmung der Größen $ \mbox{$a, c, \lambda$}$ benötigten Gleichungen

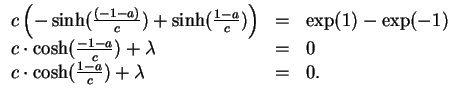
$ \mbox{$\displaystyle \begin{array}{lcl} c\left(-\sinh(\frac{(-1-a)}{c}) + \s... ...mbda & = & 0 \\ c\cdot \cosh(\frac{1-a}{c}) + \lambda & = & 0. \end{array}$}$

Aus

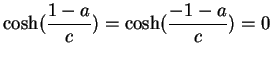
$ \mbox{$\displaystyle \cosh(\frac{1-a}{c}) = \cosh(\frac{-1-a}{c}) = 0 $}$
folgt $ \mbox{$a = 0$}$. Aus
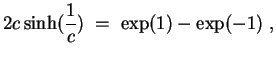
$ \mbox{$\displaystyle 2c \sinh(\frac{1}{c}) \; =\; \exp(1)-\exp(-1)\; , $}$
folgt mit $ \mbox{$\sinh(x) = \frac{\exp(x)-\exp(-x)}{2}$}$ nun $ \mbox{$c = \pm 1$}$. Die Lösung $ \mbox{$c = -1$}$ liefert die maximalen Schwerpunktshöhe.

Für $ \mbox{$c = +1$}$ wird schließlich $ \mbox{$\lambda = -\cosh(1)$}$.

Der Seilverlauf ist durch

$ \mbox{$\displaystyle y(x) = \cosh(x) - \cosh(1), \, x\in[-1,1] $}$
beschrieben.

\includegraphics [width=10cm]{s1.eps}

Das Seil hängt um $ \mbox{$\vert y(0)\vert = 1 - \cosh(1) \approx 0.54 \text{[m]}$}$ durch.