Variationsrechnung (mit Nebenbedingung).

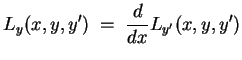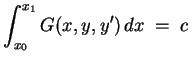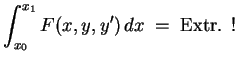
Problemstellung.

Zu lösen ist

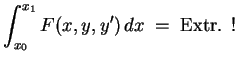
$ \mbox{$\displaystyle \int_{x_0}^{x_1} F(x,y,y')\, dx\; =\; {\mbox{Extr. !}} $}$
unter der Nebenbedingung
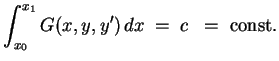
$ \mbox{$\displaystyle \int_{x_0}^{x_1} G(x,y,y')\, dx\; =\; c\; \; =\; {\mbox{const.}} $}$
Ferner sei der Rand hier stets beidseitig fixiert, d.h. sei $ \mbox{$y(x_0) = y_0$}$ und $ \mbox{$y(x_1) = y_1$}$ verlangt.

Lagrangescher Multiplikator.

Da die Nebenbedingung die Variation um einen Freiheitsgrad beschneidet, müssen wir mit einem zusätzlichen Freiheitsgrad $ \mbox{$y + \xi v + \eta w$}$ ansetzen, $ \mbox{$v$}$, $ \mbox{$w$}$ zweifach stetig differenzierbar und Null auf den Randpunkten. Dies führt auf

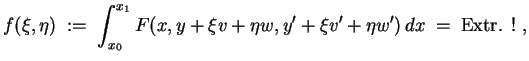
$ \mbox{$\displaystyle f(\xi,\eta)\; :=\; \int_{x_0}^{x_1} F(x,y + \xi v + \eta w,y' + \xi v' + \eta w')\, dx\; =\; {\mbox{Extr. !}}\; , $}$
unter der Nebenbedingung
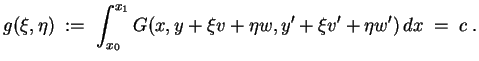
$ \mbox{$\displaystyle g(\xi,\eta) \; :=\; \int_{x_0}^{x_1} G(x,y + \xi v + \eta w,y' + \xi v' + \eta w')\, dx\; =\; c\; . $}$
Die Funktion $ \mbox{$y = y(x)$}$ stellt eine Extremale dar, falls bei $ \mbox{$(\xi,\eta) = (0,0)$}$ ein Extremum mit Nebenbedingung vorliegt für alle Testfunktionen $ \mbox{$v$}$ und $ \mbox{$w$}$. Speziell muss natürlich $ \mbox{$g(0,0) = c$}$ gelten.

Anschaulich gesprochen liefert $ \mbox{$g = c$}$ eine Kurve auf der von $ \mbox{$f$}$ beschriebenen Fläche über der $ \mbox{$\xi$}$- $ \mbox{$\eta$}$-Ebene. Damit $ \mbox{$f$}$ auf dieser Kurve in $ \mbox{$(\xi,\eta) = (0,0)$}$ ein Extremum annimmt, müssen die Gradienten von $ \mbox{$f$}$ und $ \mbox{$g$}$ dort in dieselbe Richtung zeigen - dann verschwindet die Ableitung von $ \mbox{$f$}$ in Richtung senkrecht zum Gradienten von $ \mbox{$g$}$, d.h. in Richtung tangential zu $ \mbox{$g = c$}$.

D.h. es gibt ein $ \mbox{$\lambda$}$ mit $ \mbox{$(f_\xi,f_\eta) = -\lambda (g_\xi,g_\eta)$}$ bei $ \mbox{$(\xi,\eta) = (0,0)$}$. Schreiben wir $ \mbox{$l = f + \lambda g$}$, so verlangen wir also die Existenz eines $ \mbox{$\lambda$}$ mit $ \mbox{$l_\xi = 0$}$ und $ \mbox{$l_\eta = 0$}$ an dieser Stelle.

Das Variationsproblem wird also von der Funktion $ \mbox{$y$}$ gelöst, wenn $ \mbox{$y$}$ die Nebenbedingung erfüllt, und wenn man einen Langrange-Multiplikator $ \mbox{$\lambda$}$ so findet, daß mit $ \mbox{$L = F + \lambda G$}$ die Funktion $ \mbox{$y$}$ die Euler-Lagrange-Gleichung für $ \mbox{$L$}$ erfüllt. Denn dann verschwindet die Variation von $ \mbox{$L$}$ in jede Richtung, und insbesondere ist $ \mbox{$l_\xi = 0$}$ und $ \mbox{$l_\eta = 0$}$ bei $ \mbox{$(\xi,\eta) = (0,0)$}$ für die Variationen in Richtung beliebig gewählter Testfunktionen $ \mbox{$v$}$ und $ \mbox{$w$}$.

Vorgehen.

Man stelle die Euler-Lagrange-Gleichung

$ \mbox{$\displaystyle L_y(x,y,y') \; =\; \frac{d}{dx} L_{y'}(x,y,y') $}$
auf mit $ \mbox{$L = F + \lambda G$}$ bei noch unbekanntem $ \mbox{$\lambda$}$. In der Lösung $ \mbox{$y$}$ dieser Differentialgleichung wird also neben den üblichen Konstanten der Parameter $ \mbox{$\lambda$}$ auftauchen. Diese verwende man nun, um außer den Randbedingungen auch noch die
$ \mbox{$\displaystyle \int_{x_0}^{x_1} G(x,y,y')\, dx\; =\; c\; $}$
zu erfüllen.