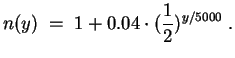Da
![]() nicht explizit von
nicht explizit von
![]() abhängt,
muß die Euler-Lagrange Bedingung
abhängt,
muß die Euler-Lagrange Bedingung
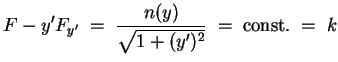
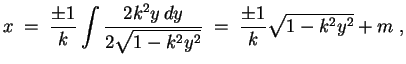
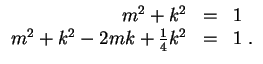
![\includegraphics [width=6cm]{s1.eps}](img13.gif)
Die Randbedingung (1) direkt in die Differentialgleichung eingesetzt, ergibt
![]() . Mit
. Mit
![]() wird schließlich
wird schließlich
![]() . Der Ansatz
. Der Ansatz
![]() liefert dann
liefert dann
![]() . Das Licht kommt also bei
. Das Licht kommt also bei
![]() zum Stillstand.
zum Stillstand.
![\includegraphics [width=6cm]{s11.eps}](img20.gif)
Bemerkung:
In der Atmosphäre wird Licht allerdings nicht entlang von Kreisbögen
gebeugt, da ein anderer Brechungsindex vorliegt:
Luft hat (auf Meereshöhe) den Brechungsindex von etwa
![]() .
Da sich der Luftdruck etwa alle
.
Da sich der Luftdruck etwa alle
![]() halbiert, gilt für
den Brechungsindex in etwa
halbiert, gilt für
den Brechungsindex in etwa