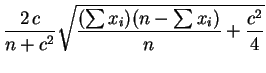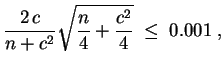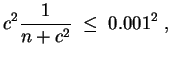Sei
![]() dazu eine Folge unabhängiger binomial-verteilter
Zufallsvariablen mit zu schätzendem Parameter
dazu eine Folge unabhängiger binomial-verteilter
Zufallsvariablen mit zu schätzendem Parameter
![]() .
.
Zunächst liest man
![]() aus
einer geeigneten Tabelle ab.
aus
einer geeigneten Tabelle ab.
Die Länge des Konfidenzintervalls zum gegebenen Konfidenzniveau
![]() ist gegeben durch
ist gegeben durch