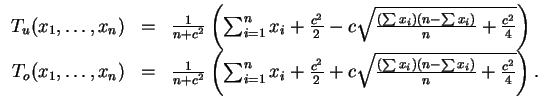Sei
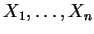 eine Stichprobe mit zu schätzendem unbekannten
Parameter
eine Stichprobe mit zu schätzendem unbekannten
Parameter
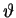 .
.
Ein Konfidenzintervall für
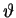 ist ein
Zufallsintervall
ist ein
Zufallsintervall
![$ \mbox{$[T_u,T_o]$}$](img3.gif) , d.h.
, d.h.
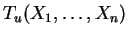 und
und
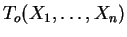 sind Schätzer für
sind Schätzer für
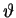 .
.
Ein Konfidenzintervall zum
Konfidenzniveau
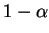 mit
mit
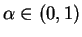 enthält den wahren Parameter
enthält den wahren Parameter
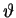 mit Wahrscheinlichkeit
mit Wahrscheinlichkeit
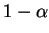 .
Unter der Annahme, die
.
Unter der Annahme, die
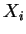 seien mit Parameter
seien mit Parameter
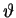 verteilt,
muß gelten
verteilt,
muß gelten
Es gibt mehrere Möglichkeiten Konfidenzintervalle zu berechnen.
- (i)
- Sei
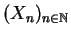 ein Folge unabhängiger und
ein Folge unabhängiger und
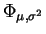 -verteilter Zufallsvariablen
mit bekannter Varianz
-verteilter Zufallsvariablen
mit bekannter Varianz
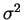 gegeben, so gilt
für das symmetrische Konfidenzintervall um
gegeben, so gilt
für das symmetrische Konfidenzintervall um
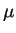 und somit
Dabei ist
und somit
Dabei ist
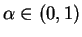 die Irrtumswahrscheinlichkeit und
die Irrtumswahrscheinlichkeit und
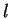 gibt die Länge des Konfidenzintervalls an.
Je nach Aufgabenstellung ist der verbleibende Parameter
(also entweder
gibt die Länge des Konfidenzintervalls an.
Je nach Aufgabenstellung ist der verbleibende Parameter
(also entweder
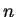 oder
oder
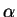 oder
oder
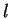 ) geeignet zu bestimmen.
) geeignet zu bestimmen.
- (ii)
- Ist von den
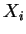 nur
nur
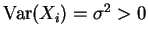 bekannt,
so folgt nach dem zentralen Grenzwertsatz, daß
bekannt,
so folgt nach dem zentralen Grenzwertsatz, daß
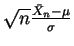 approximativ standardnormalverteilt ist, d.h. Teil (i) wird
genauso verwendet.
approximativ standardnormalverteilt ist, d.h. Teil (i) wird
genauso verwendet.
- (iii)
- Im Spezialfall binomialverteilter Zufallsvariablen mit
unbekanntem Parameter
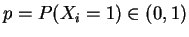 ist die Varianz durch
ist die Varianz durch
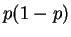 gegeben, muß also nicht als
bekannt vorausgesetzt werden, sonden geht in die Herleitung als vom unbekannten Parameter
gegeben, muß also nicht als
bekannt vorausgesetzt werden, sonden geht in die Herleitung als vom unbekannten Parameter
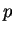 abhängig ein. Das liefert
dann aufwendigere Formeln.
abhängig ein. Das liefert
dann aufwendigere Formeln.
Da eine Binomialverteilung nach de Moivre-Laplace nach
Normierung in der Grenze gegen die Standardnormalverteilung geht,
wird mit
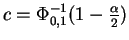 für große
für große
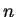
wobei
Um zu Meßdaten
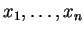 ein solches Konfidenzintervall anzugeben,
setzt man diese in obige Ausdrücke für
ein solches Konfidenzintervall anzugeben,
setzt man diese in obige Ausdrücke für
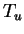 und
und
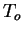 ein, dabei ist
ein, dabei ist
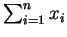 gerade die
Anzahl der Treffer.
gerade die
Anzahl der Treffer.
![]() eine Stichprobe mit zu schätzendem unbekannten
Parameter
eine Stichprobe mit zu schätzendem unbekannten
Parameter
![]() .
.
![]() ist ein
Zufallsintervall
ist ein
Zufallsintervall
![]() , d.h.
, d.h.
![]() und
und
![]() sind Schätzer für
sind Schätzer für
![]() .
.
![]() mit
mit
![]() enthält den wahren Parameter
enthält den wahren Parameter
![]() mit Wahrscheinlichkeit
mit Wahrscheinlichkeit
![]() .
Unter der Annahme, die
.
Unter der Annahme, die
![]() seien mit Parameter
seien mit Parameter
![]() verteilt,
muß gelten
verteilt,
muß gelten
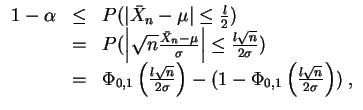
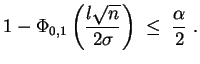
![]() für große
für große
![]()