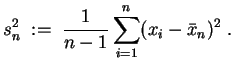Eine Stichprobe besteht aus
![]() unabhängigen und identisch
verteilten Zufallsvariablen
unabhängigen und identisch
verteilten Zufallsvariablen
![]() .
.
Überlicherweise möchte man aus Daten
![]() , die als
Realisierungen der Zufallsvariablen
, die als
Realisierungen der Zufallsvariablen
![]() aufgefaßt werden, Aussagen
über die Verteilung der
aufgefaßt werden, Aussagen
über die Verteilung der
![]() erhalten (so z.B. Mittelwert oder Varianz).
Hierfür setzt man für jedes
erhalten (so z.B. Mittelwert oder Varianz).
Hierfür setzt man für jedes
![]() eine Schätzfunktion
eine Schätzfunktion
![]() .
Deren Plausibilität wird
durch eine Betrachtung der Folge der zugehörigen Zufallsvariablen
.
Deren Plausibilität wird
durch eine Betrachtung der Folge der zugehörigen Zufallsvariablen
Um die Verteilung der
![]() sinnvoll schätzen zu können, legt man sich
auf eine Verteilungsklasse fest (z.B. Normalverteilung, Exponentialverteilung, ...).
Zu schätzen bleibt jeweils der die Verteilung beschreibende, aber noch unbekannte
reelle Parameter.
So kann beispielsweise der Erwartungswert bekannt und die Varianz zu schätzen sein.
sinnvoll schätzen zu können, legt man sich
auf eine Verteilungsklasse fest (z.B. Normalverteilung, Exponentialverteilung, ...).
Zu schätzen bleibt jeweils der die Verteilung beschreibende, aber noch unbekannte
reelle Parameter.
So kann beispielsweise der Erwartungswert bekannt und die Varianz zu schätzen sein.
Eine sinnvolle Schätzfunktion sollte folgende Kriterien erfüllen.
Hierbei folgt aus Erwartungstreue i.a. keine Konsistenz und aus Konsistenz i.a. keine Erwartungstreue.
Folgende Schätzfunktionen sind für die Anwendung von Bedeutung.
Der (empirische) Mittelwert ist definiert durch
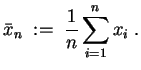
Die (empirische) Varianz ist (für
![]() ) definiert durch
) definiert durch