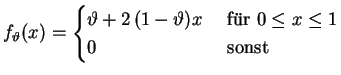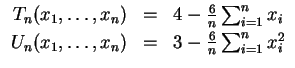Gegeben sei eine Stichprobe
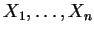 , wobei die Dichte
der
, wobei die Dichte
der
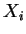 abhängig von einem zu schätzenden Parameter
abhängig von einem zu schätzenden Parameter
![$ \mbox{$\vartheta\in[0,2]$}$](img3.gif) durch
durch
gegeben sei.
- Berechne für festes
![$ \mbox{$\vartheta\in[0,2]$}$](img3.gif) die Größen
die Größen
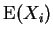 ,
,
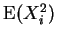 und
und
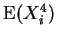 .
.
- Zeige daß die beiden Schätzfunktionen
erwartungstreu und konsistent für
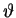 sind.
sind.
- Gebe in Abhängigkeit von
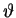 an, welcher Schätzer die geringere Varianz hat (d.h. genauer ist).
an, welcher Schätzer die geringere Varianz hat (d.h. genauer ist).
![]() , wobei die Dichte
der
, wobei die Dichte
der
![]() abhängig von einem zu schätzenden Parameter
abhängig von einem zu schätzenden Parameter
![]() durch
durch