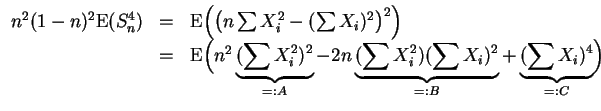
In
![]() treten
treten
![]() Terme
der Form
Terme
der Form
![]() auf (nämlich
auf (nämlich
![]() ). Das ergibt eine Beitrag
). Das ergibt eine Beitrag
![]() zu
zu
![]() .
Es treten
.
Es treten
![]() Terme der Form
Terme der Form
![]() (
(
![]() ) auf. Das ergibt eine Beitrag
) auf. Das ergibt eine Beitrag
![]() zu
zu
![]() .
.
Damit gilt
![]() .
.
Verfahre mit
![]() und
und
![]() analog.
analog.
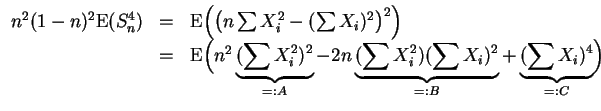
In
![]() treten
treten
![]() Terme
der Form
Terme
der Form
![]() auf (nämlich
auf (nämlich
![]() ). Das ergibt eine Beitrag
). Das ergibt eine Beitrag
![]() zu
zu
![]() .
Es treten
.
Es treten
![]() Terme der Form
Terme der Form
![]() (
(
![]() ) auf. Das ergibt eine Beitrag
) auf. Das ergibt eine Beitrag
![]() zu
zu
![]() .
.
Damit gilt
![]() .
.
Verfahre mit
![]() und
und
![]() analog.
analog.
Es ist eine längere Rechnung.