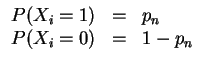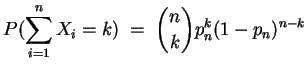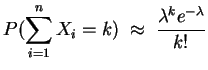Gesetze der großen Zahlen
Im folgenden sei
![]() eine unabhängige Folge von Zufallsvariablen.
eine unabhängige Folge von Zufallsvariablen.
In der Praxis kann
![]() etwa das Meßergebnis der
etwa das Meßergebnis der
![]() -ten Messung eines
beliebig oft wiederholbaren Versuchs darstellen. Liegt etwa daß Meßergebnis
stets zwischen
-ten Messung eines
beliebig oft wiederholbaren Versuchs darstellen. Liegt etwa daß Meßergebnis
stets zwischen
![]() und
und
![]() , so kann man den
Wahrscheinlichkeitsraum
, so kann man den
Wahrscheinlichkeitsraum
![]() verwenden. Ein
Elementarereignis
verwenden. Ein
Elementarereignis
![]() ist also eine Folge von Meßwerten.
Die Funktion
ist also eine Folge von Meßwerten.
Die Funktion
![]() greift dann den
greift dann den
![]() -ten Meßwert
heraus und trägt in auf der Skala
-ten Meßwert
heraus und trägt in auf der Skala
![]() ab.
ab.
Berechnet man eine Größe als Mittelwert von Einzelmessungen, so wird sich dieser Durchschnitt im allgemeinen durch Versuchswiederholung stabilisieren. Im Wahrscheinlichkeitsmodell kann man unter gewissen Voraussetzungen eine solche Stabilisierung mathematisch fassen und beweisen (Gesetze der großen Zahlen).
Das starke Gesetz der großen Zahlen besagt in Worten,
daß die Folge der Mittelwerte einer unabhängig verteilten
Zufallsvariablenfolge
![]() mit konstantem Erwartungswert
mit konstantem Erwartungswert
![]() und
konstanter Varianz
und
konstanter Varianz
![]() mit Wahrscheinlichkeit
mit Wahrscheinlichkeit
![]() gegen den Erwartungswert
gegen den Erwartungswert
![]() konvergiert.
Sei hierzu
konvergiert.
Sei hierzu
![]() der Mittelwert
der ersten
der Mittelwert
der ersten
![]() Zufallsvariablen. Es existiert
der Mittelwert der ganzen Folge
Zufallsvariablen. Es existiert
der Mittelwert der ganzen Folge
![]() und
es gilt
und
es gilt
Hieraus folgt das schwache Gesetz der großen Zahlen
Zentraler Grenzwertsatz
Betrachte die folgende Dichtefunktion für vorgegebene
![]() und
und
![]() .
.
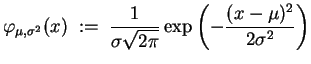
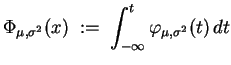
Sind hierbei
![]() und
und
![]() , so spricht man von einer
Standardnormalverteilung.
, so spricht man von einer
Standardnormalverteilung.
Sei
![]() eine identisch und gleichverteilte Folge von
Zufallsvariablen mit
eine identisch und gleichverteilte Folge von
Zufallsvariablen mit
![]() und
und
![]() .
Identisch verteilt heiße hierbei, daß die zu
.
Identisch verteilt heiße hierbei, daß die zu
![]() gehörige
Verteilungsfunktion nicht von
gehörige
Verteilungsfunktion nicht von
![]() abhängt.
abhängt.
Die durch
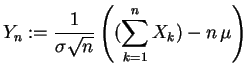
Der zentrale Grenzwertsatz besagt nun,
daß unabhängig von den weiteren Eigenschaften der
Verteilungsfunktion der
![]() die Folge
die Folge
![]() der Verteilungen der
der Verteilungen der
![]() gegen die Verteilung der
Standardnormalverteilung konvergiert, d.h.
gegen die Verteilung der
Standardnormalverteilung konvergiert, d.h.
Grenzwertsatz von de Moivre-Laplace
Wir wollen den zentralen Grenzwertsatz nun auf eine
unabhängige Folge von Zufallsvariablen
![]() mit
mit
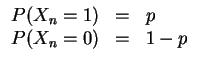
Nach dem Grenzwertsatz von de Moivre-Laplace gilt nun für
![]()
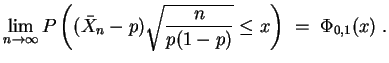
In der Praxis wird diese Formel wie folgt für große
![]() zur Approximation von
zur Approximation von
![]() verwandt, wobei
verwandt, wobei
![]() entsprechend zu verrechnen ist.
entsprechend zu verrechnen ist.
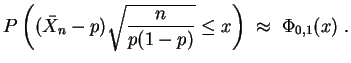
Grenzwertsatz von Poisson
Sei
![]() eine Folge reeller Zahlen
eine Folge reeller Zahlen
![]() mit
mit
![]() . Dann ist
. Dann ist
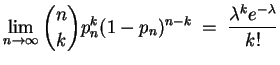
Für ein festes
![]() sei eine unabhängige Folge von
Zufallsvariablen
sei eine unabhängige Folge von
Zufallsvariablen
![]() mit
mit