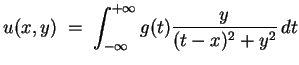Eine zweifach differenzierbare Funktion
![]() von der offenen Menge
von der offenen Menge
![]() nach
nach
![]() heißt harmonisch, falls
heißt harmonisch, falls
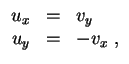
Sei
![]() , sei
, sei
![]() eine stetige Funktion.
Gesucht ist eine stetige Funktion
eine stetige Funktion.
Gesucht ist eine stetige Funktion
![]() welche auf
welche auf
![]() harmonisch ist, und welche der Randbedingung
harmonisch ist, und welche der Randbedingung
![]() genügt.
genügt.
Dieses Dirichletproblem hat als eindeutige Lösung die folgende Funktion.
Sei
![]() , sei
, sei
![]() . Sei
der Poissonkern gegeben durch
. Sei
der Poissonkern gegeben durch
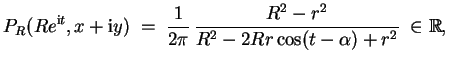
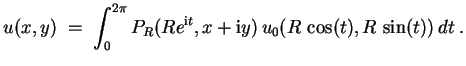
Eine Möbiustransformation der oberen Halbebene
![]() auf den Einheitskreis liefert dazuhin folgende Aussage.
auf den Einheitskreis liefert dazuhin folgende Aussage.
Sei
![]() stetig mit
stetig mit
![]() . Dann ist die Dirichletsche Randwertaufgabe
. Dann ist die Dirichletsche Randwertaufgabe
![]() auf
auf
![]() ,
,
![]() für
für
![]() , eindeutig durch
, eindeutig durch