Kurvenintegrale.

Sei $ \mbox{$f(z)$}$ eine im Gebiet $ \mbox{$G\subseteq \mathbb{C}$}$ holomorphe, d.h. komplex differenzierbare Funktion. Sei $ \mbox{$\gamma:[a,b]\to\mathbb{C}$}$ eine stetige und stückweise differenzierbare Funktion. Interpretiert man $ \mbox{$[a,b]$}$ als Zeitintervall, so ist $ \mbox{$\gamma$}$ ein in der Zeit von $ \mbox{$a$}$ bis $ \mbox{$b$}$ durchlaufener Weg in $ \mbox{$\mathbb{C}$}$, $ \mbox{$\gamma(t)$}$ der Aufenthaltsort zum Zeitpunkt $ \mbox{$t$}$, und $ \mbox{$\gamma'(t)$}$ der Geschwindigkeitsvektor beim Durchlaufen zum Zeitpunkt $ \mbox{$t$}$. In anderen Worten, $ \mbox{$\gamma$}$ bezeichnet nicht nur den durchschrittenen Weg in $ \mbox{$\mathbb{C}$}$, sondern beschreibt auch die Art und Weise, wie er durchlaufen wird.

Wir definieren das Wegintegral von $ \mbox{$f$}$ entlang $ \mbox{$\gamma$}$ als

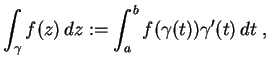
$ \mbox{$\displaystyle \int_\gamma f(z)\, dz := \int_a^b f(\gamma(t))\gamma'(t)\,dt\; , $}$
d.h. unter Berücksichtigung von $ \mbox{$\frac{dz}{dt} = \gamma'(t)$}$.

Dieses Integral ist nun in folgendem Sinne wegunabhängig. Sei $ \mbox{$\tilde \gamma$}$ ein weiterer Weg mit $ \mbox{$\tilde \gamma(a) = \gamma(a)$}$ und $ \mbox{$\tilde \gamma(b) = \gamma(b)$}$, also mit übereinstimmendem Anfangs- und Endpunkt. Sei die zwischen $ \mbox{$\tilde \gamma$}$ und $ \mbox{$\gamma$}$ gelegene Teilmenge von $ \mbox{$\mathbb{C}$}$ in $ \mbox{$G$}$ enthalten (genauer, es gebe eine Homotopie, die $ \mbox{$\gamma$}$ in $ \mbox{$\gamma'$}$ innerhalb $ \mbox{$G$}$ überführt). Dann ist $ \mbox{$\int_\gamma f(z)\, dz = \int_{\tilde \gamma} f(z)\, dz$}$.