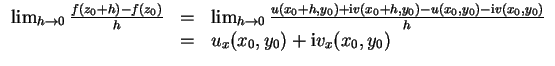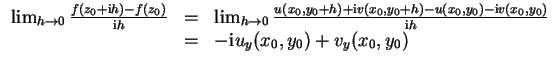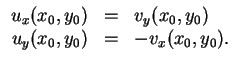Sei
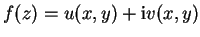 eine komplexwertige Funktion,
eine komplexwertige Funktion,
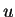 und
und
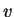 reellwertig,
reellwertig,
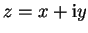 ,
,
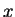 ,
,
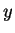 reell.
Sei
reell.
Sei
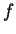 in
in
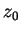 differenzierbar, d.h. existiere der Grenzwert
differenzierbar, d.h. existiere der Grenzwert
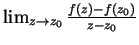 .
.
Insbesondere stimmt
mit
überein, wobei
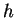 eine reelle Variable bezeichne und
eine reelle Variable bezeichne und
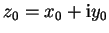 geschrieben wird mit
geschrieben wird mit
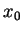 und
und
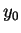 reell.
Abgleich von Real- und Imaginärteil liefert die
Cauchy-Riemannschen Differentialgleichungen
Ist
reell.
Abgleich von Real- und Imaginärteil liefert die
Cauchy-Riemannschen Differentialgleichungen
Ist
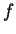 in jedem Punkt eines Gebiets
in jedem Punkt eines Gebiets
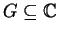 differenzierbar, so sagt man auch,
differenzierbar, so sagt man auch,
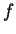 ist holomorph auf
ist holomorph auf
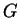 . Ein Gebiet bezeichnet hierbei eine offene,
zusammenhängende Teilmenge von
. Ein Gebiet bezeichnet hierbei eine offene,
zusammenhängende Teilmenge von
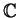 .
.
![]() eine komplexwertige Funktion,
eine komplexwertige Funktion,
![]() und
und
![]() reellwertig,
reellwertig,
![]() ,
,
![]() ,
,
![]() reell.
Sei
reell.
Sei
![]() in
in
![]() differenzierbar, d.h. existiere der Grenzwert
differenzierbar, d.h. existiere der Grenzwert
![]() .
.