Lösung.

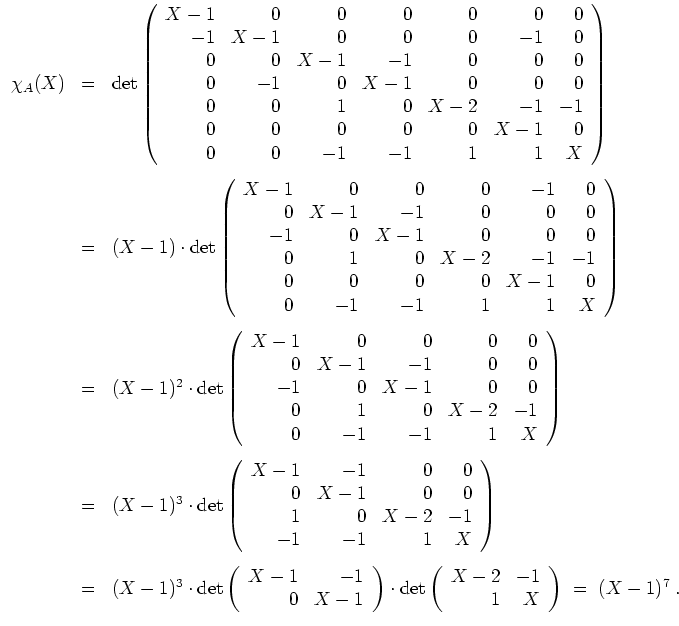
Das charakteristische Polynom ergibt sich zu

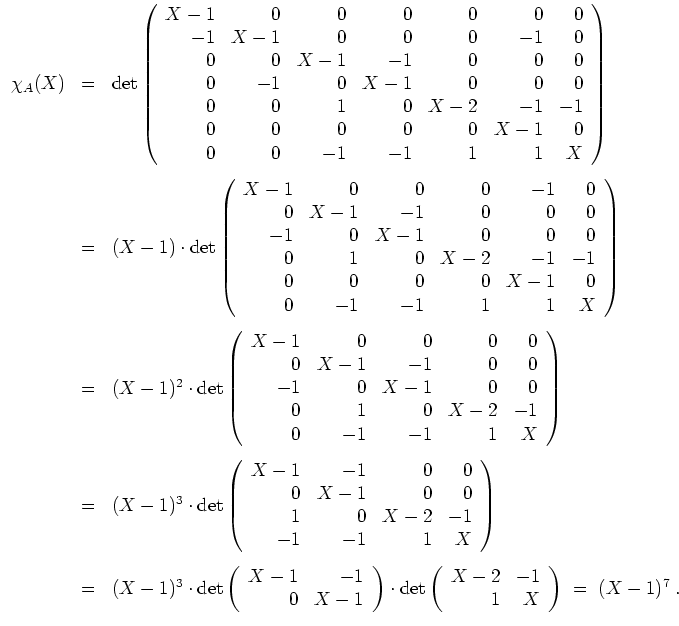
$ \mbox{$\displaystyle \begin{array}{rcl} \chi_A(X) & = & \det\left( \begin{ar... ... -1 \\ 1 & X \\ \end{array}\right) \; = \; (X - 1)^7\; .\\ \end{array}$}$

Wir haben also $ \mbox{$1$}$ als einzigen Eigenwert, und dieser hat die algebraische Vielfachheit $ \mbox{$7$}$ .

Sei

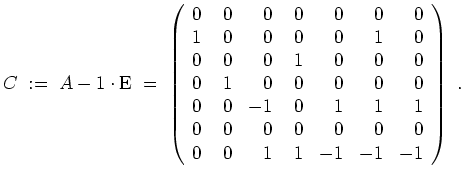
$ \mbox{$\displaystyle C \; :=\; A - 1\cdot\text{E} \; = \; \left( \begin{arra... ... 0 & 0 & 0 & 0 \\ 0 & 0 & 1 & 1 &-1 &-1 & -1 \\ \end{array}\right) \; . $}$
Es wird
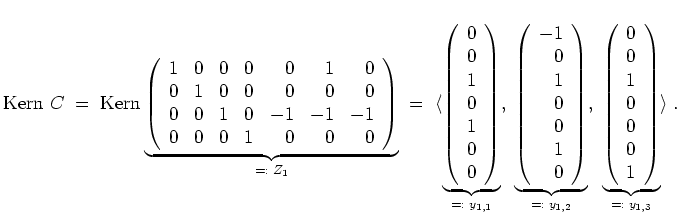
$ \mbox{$\displaystyle \text{Kern }C \; = \; \text{Kern} \underbrace{ \left( \b... ... 0\\ 0\\ 0\\ 1\\ \end{array}\right)}_{=:\; y_{1,3}} \rangle\; . $}$
Es wird
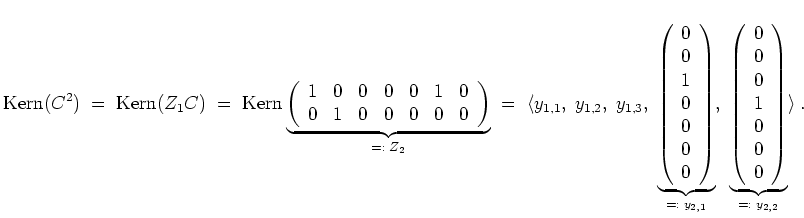
$ \mbox{$\displaystyle \text{Kern}(C^2)\; =\; \text{Kern}(Z_1 C) \; = \; \text... ... 1\\ 0\\ 0\\ 0\\ \end{array}\right)}_{=:\; y_{2,2}} \rangle\; . $}$
Es wird
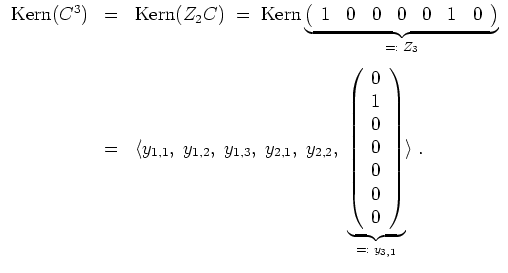
$ \mbox{$\displaystyle \begin{array}{rcl} \text{Kern}(C^3) &=& \text{Kern}(Z_2 ... ...\\ 0\\ 0\\ \end{array}\right)}_{=:\; y_{3,1}} \rangle\; . \end{array}$}$
Es wird
$ \mbox{$\displaystyle \begin{array}{rcl} \text{Kern}(C^4) &=& \text{Kern}(Z_3 ... ...{=:\; y_{4,1}} \rangle\; =\; \text{H}_A(1)\; =\; \mathbb{C}^7\; . \end{array}$}$

Sei $ \mbox{$x_{4,1} := y_{4,1}$}$ .

Es ist (zufällig) $ \mbox{$C x_{4,1} = y_{3,1}$}$ . Es sind keine Vektoren aus $ \mbox{$(y_{3,1})$}$ auszuwählen, es ist $ \mbox{$(y_{1,1},y_{1,2},y_{1,3},y_{2,1},y_{2,2},C x_{4,1})$}$ bereits eine Basis von $ \mbox{$\text{Kern}(C^3)$}$ .

Es ist (zufällig) $ \mbox{$C^2 x_{4,1} = y_{2,2}$}$ . Wir können den Vektor $ \mbox{$x_{2,1} := y_{2,1}$}$ aus $ \mbox{$(y_{2,1},y_{2,2})$}$ auswählen, um eine Basis $ \mbox{$(y_{1,1},y_{1,2},y_{1,3},C^2 x_{4,1}, x_{2,1})$}$ von $ \mbox{$\text{Kern}(C^2)$}$ zu erhalten.

Es werden

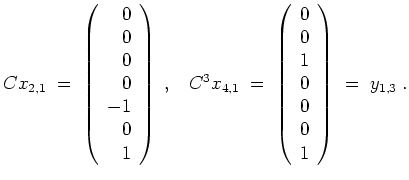
$ \mbox{$\displaystyle C x_{2,1} \; =\; \left( \begin{array}{r} 0\\ 0\\ ... ... 1\\ 0\\ 0\\ 0\\ 1\\ \end{array}\right) \; =\; y_{1,3} \; . $}$
Wir können den Vektor $ \mbox{$x_{1,1} := y_{1,2}$}$ aus $ \mbox{$(y_{1,1},y_{1,2},y_{1,3})$}$ auswählen, um eine Basis $ \mbox{$(C^3 x_{4,1},C x_{2,1}, x_{1,1})$}$ von $ \mbox{$\text{Kern}(C^1)$}$ zu erhalten.

Insgesamt bilden die Tupel $ \mbox{$\text{Kette}(x_{4,1})$}$ , $ \mbox{$\text{Kette}(x_{2,1})$}$ und $ \mbox{$\text{Kette}(x_{1,1})$}$ eine Basis

$ \mbox{$\displaystyle (C^3 x_{4,1},\; C^2 x_{4,1},\; C x_{4,1},\; x_{4,1},\; C x_{2,1},\; x_{2,1},\; x_{1,1} ) $}$
von $ \mbox{$\text{H}_A(1)$}$ , deren Vektoren wir in eine Matrix
$ \mbox{$\displaystyle S \; :=\; \left( \begin{array}{rrrrrrr} 0 &\; 0 &\; 0 &... ...& 0 & 0 & 0 & 0 & 1 \\ 1 & 0 & 0 & 0 & 1 & 0 & 0 \\ \end{array}\right) $}$
eintragen können. Dann ist
$ \mbox{$\displaystyle S^{-1} A S \; =\; \left( \begin{array}{rrrrrrr} 1 & 1 ... ...1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array}\right) \; =: \; J\; . $}$

Insbesondere ist

$ \mbox{$\displaystyle e^{tJ} \; =\; e^t\cdot \left( \begin{array}{ccccccc} 1 ... ...& 0 & 0 & 1 & 0 \\ 0 & 0 & 0 & 0 & 0 & 0 & 1 \\ \end{array}\right) \; . $}$

Somit erhalten wir als allgemeine Lösung der homogenen Gleichung $ \mbox{$u'(t) = A u(t)$}$ den Funktionenvektor

$ \mbox{$\displaystyle u(t) \; =\; S e^{tJ} c \; =\; e^t\cdot \left( \begin{ar... ...0 & 1 \\ 1 & t & t^2/2 & t^3/6 & 1 & t & 0 \\ \end{array}\right)\cdot c $}$
für $ \mbox{$c\in\mathbb{C}^7$}$ beliebig.

In der partikuläre Lösung taucht der Ausdruck $ \mbox{$S^{-1} b$}$ auf. Es ist nicht erforderlich, die Inverse $ \mbox{$S^{-1}$}$ komplett zu berechnen, es ist einfacher, $ \mbox{$S^{-1} b$}$ als Lösung von $ \mbox{$S(S^{-1}b) = b$}$ zu bestimmen. (Dies ist immer dann ratsam, wenn der Vektor $ \mbox{$b$}$ ein Vielfaches eines konstanten Vektors ist.) Wir erhalten

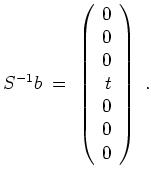
$ \mbox{$\displaystyle S^{-1} b \; =\; \left( \begin{array}{r} 0\\ 0\\ 0\\ t\\ 0\\ 0\\ 0\\ \end{array}\right)\; . $}$
Als partikuläre Lösung der inhomogenen Gleichung $ \mbox{$u'(t) = A u(t) + b$}$ ergibt sich der Funktionenvektor
$ \mbox{$\displaystyle \begin{array}{rcl} u_0(t) & = & S e^{tJ}\displaystyle\i... ...4\\ -t - 3\\ 0\\ 0\\ t + 4\\ \end{array}\right)\; . \end{array}$}$

Die allgemeine Lösung der inhomogenen Gleichung $ \mbox{$u'(t) = A u(t) + b(t)$}$ setzt sich dann zusammen zu

$ \mbox{$\displaystyle u(t) \; =\; u_0(t) + S e^{tJ} c $}$
für $ \mbox{$c\in\mathbb{C}^7$}$ beliebig.