Es ist
zu lösen.
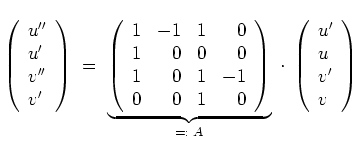
Berechnen wir die Jordanform von
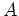 . Zunächst wird
. Zunächst wird
Es ist
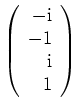 ein Eigenvektor zum Eigenwert
ein Eigenvektor zum Eigenwert
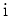 , und
, und
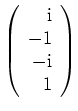 ein Eigenvektor zum Eigenwert
ein Eigenvektor zum Eigenwert
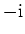 .
.
Beim Eigenwert
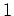 berechnen wir eine Zeilenstufenform
berechnen wir eine Zeilenstufenform
von
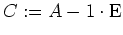 , was die Basis
, was die Basis
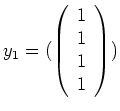 von
von
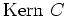 liefert. Ferner berechnen wir eine Zeilenstufenform
von
liefert. Ferner berechnen wir eine Zeilenstufenform
von
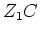 , was die Basisergänzung
, was die Basisergänzung
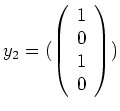 von
von
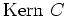 zu
zu
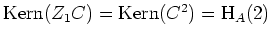 liefert. Mit
liefert. Mit
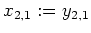 bilden wir die Kette
bilden wir die Kette
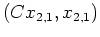 (in welcher zufällig
(in welcher zufällig
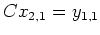 ist) und erhalten mit
die Jordanform
und somit
was uns zu der ein Fundamentalsystem in ihren Spalten beinhaltenden Matrix
Die mit
ist) und erhalten mit
die Jordanform
und somit
was uns zu der ein Fundamentalsystem in ihren Spalten beinhaltenden Matrix
Die mit
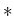 gekennzeichneten Einträge sind redundant, da nämlich jeweils die Ableitung des darunterstehenden Eintrags. Sie dennoch auszurechnen, kann man als Probe durchführen.
gekennzeichneten Einträge sind redundant, da nämlich jeweils die Ableitung des darunterstehenden Eintrags. Sie dennoch auszurechnen, kann man als Probe durchführen.
Wir erhalten als allgemeine Lösung
mit
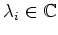 beliebig, oder, umgeformt,
mit
beliebig, oder, umgeformt,
mit
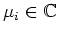 beliebig.
beliebig.
Alternativ kann man auch
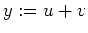 und
und
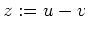 setzen, und das System
setzen, und das System
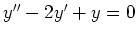 ,
,
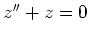 lösen. Ein solcher Trick ist allerdings selten anwendbar.
lösen. Ein solcher Trick ist allerdings selten anwendbar.

![]() . Zunächst wird
. Zunächst wird
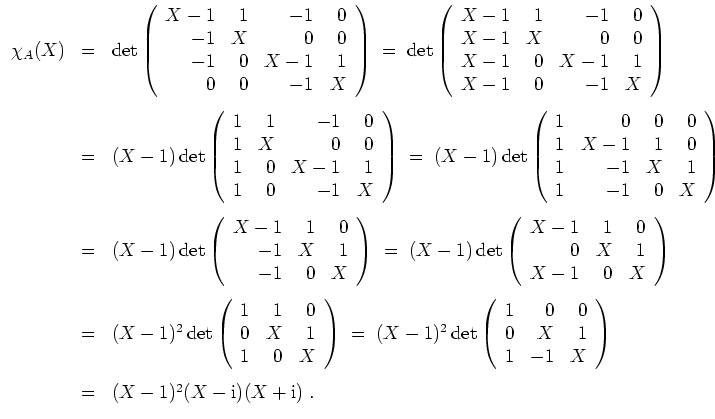
 ein Eigenvektor zum Eigenwert
ein Eigenvektor zum Eigenwert
![]() , und
, und
 ein Eigenvektor zum Eigenwert
ein Eigenvektor zum Eigenwert
![]() .
.
![]() berechnen wir eine Zeilenstufenform
berechnen wir eine Zeilenstufenform
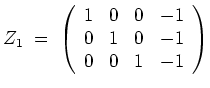
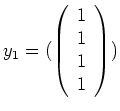 von
von
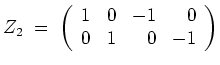
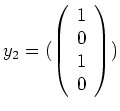 von
von
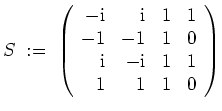
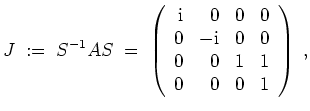
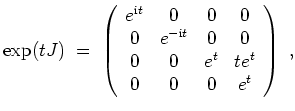
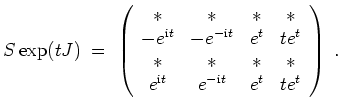
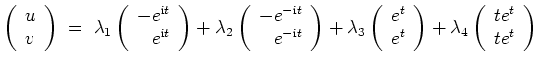
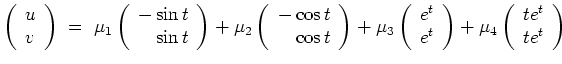
![]() und
und
![]() setzen, und das System
setzen, und das System
![]() ,
,
![]() lösen. Ein solcher Trick ist allerdings selten anwendbar.
lösen. Ein solcher Trick ist allerdings selten anwendbar.