Lösung.

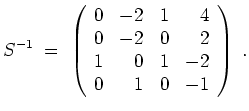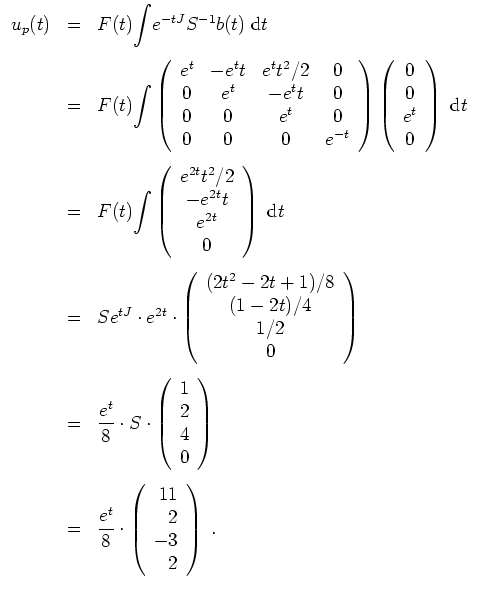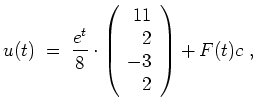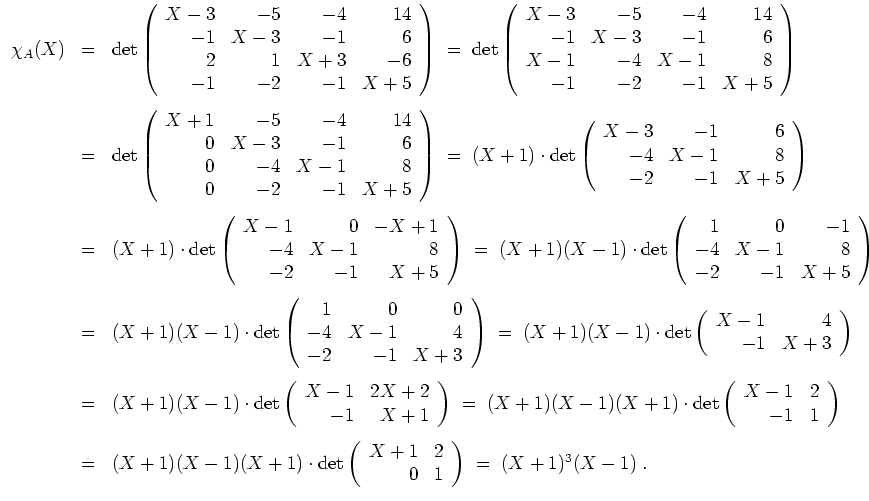
Es wird

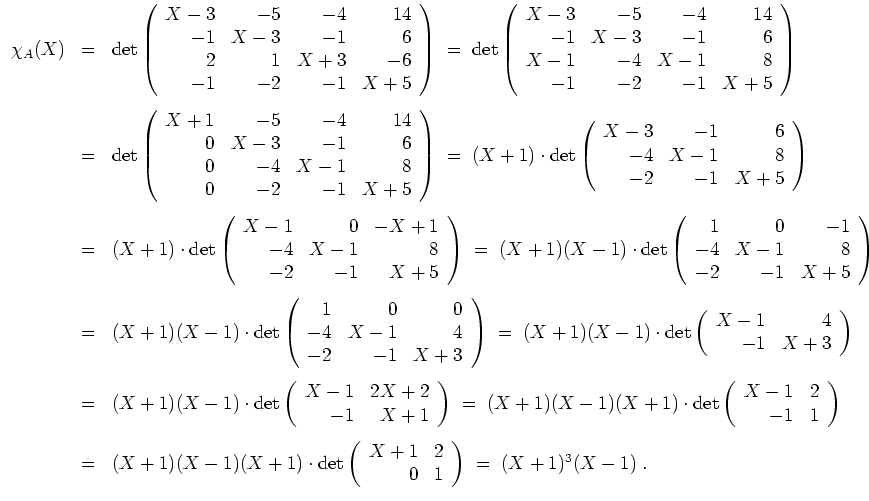
$ \mbox{$\displaystyle \begin{array}{rcl} \chi_A(X) & = & \det\left( \begin{ar... ... 0 & 1 \\ \end{array} \right) \; =\; (X+1)^3(X-1) \; . \\ \end{array}$}$

Beim Eigenwert $ \mbox{$1$}$ erhalten wir

$ \mbox{$\displaystyle \text{Kern}\left( \begin{array}{rrrr} 2 & 5 & 4 &-14 \\... ... 2 \\ 0 \\ 1 \\ \end{array}\right) \rangle \; = \; \text{H}_A(1) \; . $}$

Beim Eigenwert $ \mbox{$-1$}$ setzen wir zunächst

$ \mbox{$\displaystyle C \; =\; A + \text{E} \; = \; \left( \begin{array}{rrrr}... ... 1 & -6 \\ -2 &-1 &-2 & 6 \\ 1 & 2 & 1 & -4 \\ \end{array}\right)\; . $}$
Wir erhalten
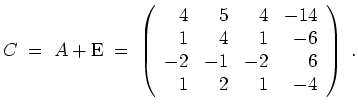
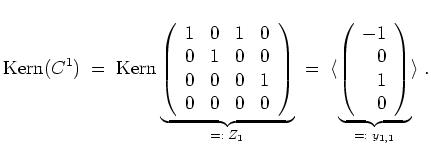
$ \mbox{$\displaystyle \text{Kern}(C^1) \; = \; \text{Kern}\underbrace{\left( ... ...\\ 0 \\ 1 \\ 0 \\ \end{array}\right)}_{=:\; y_{1,1}} \rangle \; . $}$

Ferner wird

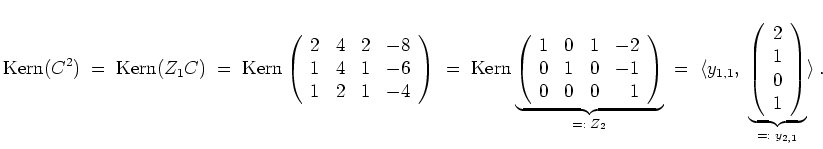
$ \mbox{$\displaystyle \text{Kern}(C^2) \; = \; \text{Kern}(Z_1 C) \; = \; \te... ...\\ 1 \\ 0 \\ 1 \\ \end{array}\right)}_{=:\; y_{2,1}} \rangle \; . $}$

Schließlich wird

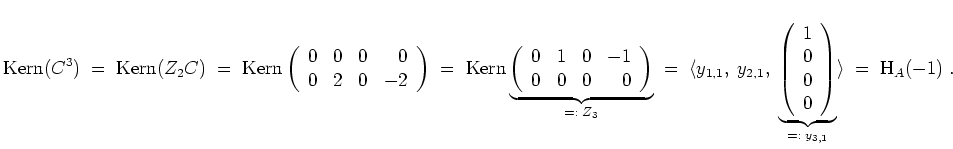
$ \mbox{$\displaystyle \text{Kern}(C^3) \; = \; \text{Kern}(Z_2 C) \; = \; \te... ...0 \\ \end{array}\right)}_{=:\; y_{3,1}} \rangle \; = \; \text{H}_A(-1)\; . $}$

Wählen wir $ \mbox{$x_{3,1} := y_{3,1}$}$ , so sind schon aus Dimensionsgründen in den Stufen $ \mbox{$2$}$ und $ \mbox{$1$}$ keine weiteren Vektoren auszuwählen. Der Eigenwert $ \mbox{$-1$}$ liefert also die Kette

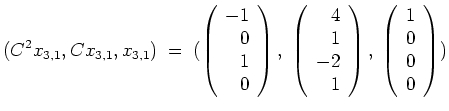
$ \mbox{$\displaystyle (C^2 x_{3,1}, C x_{3,1}, x_{3,1}) \; = \; (\left( \begi... ... \left( \begin{array}{r} 1 \\ 0 \\ 0 \\ 0 \\ \end{array}\right)) $}$
als Beitrag zur Matrix $ \mbox{$S$}$ .

Insgesamt erhalten wir mit

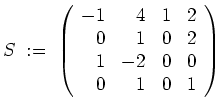
$ \mbox{$\displaystyle S \; :=\; \left( \begin{array}{rrrr} -1 & 4 & 1 & 2 \\ ... ... & 1 & 0 & 2 \\ 1 &-2 & 0 & 0 \\ 0 & 1 & 0 & 1 \\ \end{array}\right) $}$
die Jordanform
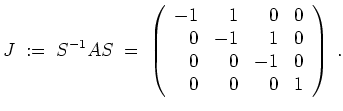
$ \mbox{$\displaystyle J \; :=\; S^{-1} A S \; = \; \left( \begin{array}{rrrr} ... ... & 1 & 0 \\ 0 & 0 &-1 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right)\; . $}$

Somit erhalten wir

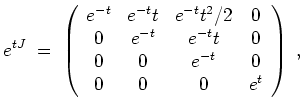
$ \mbox{$\displaystyle e^{tJ} \; = \; \left( \begin{array}{cccc} e^{-t} & e^{... ...0 \\ 0 & 0 & e^{-t} & 0 \\ 0 & 0 & 0 & e^t \\ \end{array}\right)\; , $}$
also für die allgemeine Lösung der zugehörigen homogenen Differentialgleichung die Fundamentalmatrix
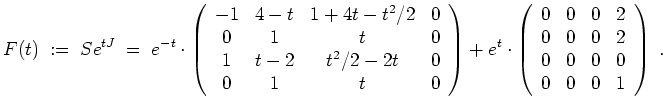
$ \mbox{$\displaystyle F(t) \; := \; S e^{tJ} \; = \; e^{-t}\cdot \left( \begi... ...& 0 & 2 \\ 0 & 0 & 0 & 0 \\ 0 & 0 & 0 & 1 \\ \end{array}\right) \; . $}$

Bestimmen wir nun eine partikuläre Lösung der inhomogenen Gleichung. Hierzu berechnen wir zunächst

$ \mbox{$\displaystyle S^{-1} \; = \; \left( \begin{array}{rrrr} 0 & -2 & 1 & ... ... 0 & 2 \\ 1 & 0 & 1 & -2 \\ 0 & 1 & 0 & -1 \\ \end{array}\right)\; . $}$
Sodann wird die partikuläre Lösung
$ \mbox{$\displaystyle \begin{array}{rcl} u_p(t) & = & F(t) {\displaystyle\int}... ...r} 11 \\ 2 \\ -3 \\ 2 \\ \end{array}\right) \; . \\ \end{array}$}$
Somit ist die allgemeine Lösung von der Form
$ \mbox{$\displaystyle u(t) \; = \; \dfrac{e^t}{8}\cdot \left( \begin{array}{r} 11 \\ 2 \\ -3 \\ 2 \\ \end{array}\right) + F(t) c\; , $}$
wobei $ \mbox{$F(t)$}$ wie oben beschrieben sei, und wobei $ \mbox{$c\in\mathbb{C}^4$}$ ein beliebig wählbarer Vektor ist.