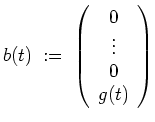Differentialgleichungen vom Typ
![]() . Homogene lineare Systeme mit konstanten Koeffizienten.
. Homogene lineare Systeme mit konstanten Koeffizienten.
Es sei
![]() ,
,
![]() . Wir suchen die vektorwertigen differenzierbaren Funktionen
. Wir suchen die vektorwertigen differenzierbaren Funktionen
![]() ,
,
![]() , die der Differentialgleichung
, die der Differentialgleichung
Eine Matrix
![]() , deren Einträge von
, deren Einträge von
![]() abhängen, und deren Spalten eine
abhängen, und deren Spalten eine
![]() -lineare Basis von
-lineare Basis von
![]() bilden,
nennt man Fundamentalmatrix dieser Differentialgleichung. So ist z.B.
bilden,
nennt man Fundamentalmatrix dieser Differentialgleichung. So ist z.B.
![]() eine Fundamentalmatrix von
eine Fundamentalmatrix von
![]() .
Jede Lösung dieser Differentialgleichung läßt sich dann eindeutig in der Form
.
Jede Lösung dieser Differentialgleichung läßt sich dann eindeutig in der Form
![]() für ein
für ein
![]() darstellen.
darstellen.
In der Praxis berechnet man nun eine Matrix
![]() in Jordanform mit
in Jordanform mit
Differentialgleichungen vom Typ
![]() . Inhomogene lineare Systeme mit konstanten Koeffizienten.
. Inhomogene lineare Systeme mit konstanten Koeffizienten.
Sei nun zusätzlich eine differenzierbare Funktion
![]() gegeben. Die Lösungsgesamtheit
gegeben. Die Lösungsgesamtheit
![]() der Differentialgleichung
der Differentialgleichung
Sämtliche Lösungen sind also von der Form
Um eine partikuläre Lösung zu finden, verwendet man die Methode der Variation der Konstanten.
Diese sieht den Ansatz
![]() mit einer Fundamentalmatrix
mit einer Fundamentalmatrix
![]() des zugehörigen
homogenen Systems vor.
des zugehörigen
homogenen Systems vor.
Differenziert man diesen Ausdruck, so erhält man
Man hat also mit
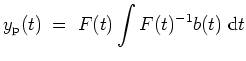
Verwendet man speziell die Fundamentalmatrix
![]() , so ist
, so ist
![]() . Verwendet man hingegen die Fundamentalmatrix
. Verwendet man hingegen die Fundamentalmatrix
![]() , so ist
, so ist
![]() .
.
Homogene lineare Differentialgleichungen
![]() -ter Ordnung mit konstanten Koeffizienten.
-ter Ordnung mit konstanten Koeffizienten.
Die Lösungsgesamtheit aller
![]() -mal differenzierbaren Funktionen
-mal differenzierbaren Funktionen
![]() , die der
homogenen linearen Differentialgleichung
, die der
homogenen linearen Differentialgleichung
![]() -ter Ordnung mit konstanten Koeffizienten
-ter Ordnung mit konstanten Koeffizienten
Wir konstruieren eine Basis dieses Vektorraumes wie folgt.
Es sei das zugehörige charakteristische Polynom
vollständig faktorisiert zu
wobei
![]() paarweise verschieden sind.
paarweise verschieden sind.
Dann ist eine Basis dieser Lösungsgesamtheit gegeben durch
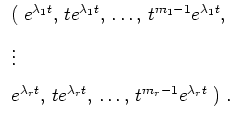
Diese Basis ist im allgemeinen komplexwertig.
Sind alle
![]() reell, und ist man an einer reellwertigen Basis der Lösungsgesamtheit interessiert, so geht man wie folgt vor.
Es sei abermals das zugehörige charakteristische Polynom vollständig faktorisiert zu
reell, und ist man an einer reellwertigen Basis der Lösungsgesamtheit interessiert, so geht man wie folgt vor.
Es sei abermals das zugehörige charakteristische Polynom vollständig faktorisiert zu
jedoch mit paarweise verschiedenen
![]() ,
,
![]() mit
mit
![]() für
für
![]() .
Dabei seien die Nullstellen so geordnet, daß
.
Dabei seien die Nullstellen so geordnet, daß
![]() und
und
![]() .
Dann ist eine reellwertige Basis der Lösungsgesamtheit gegeben durch
.
Dann ist eine reellwertige Basis der Lösungsgesamtheit gegeben durch
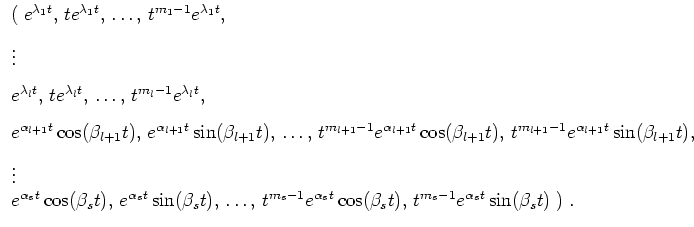
Reduktion auf ein System erster Ordnung.
Wir möchten den Zusammenhang der homogenen linearen Differentialgleichung
![]() -ter Ordnung mit konstanten Koeffizienten
mit homogenen linearen Systemen von Differentialgleichungen mit konstanten Koeffizienten nicht verschweigen.
-ter Ordnung mit konstanten Koeffizienten
mit homogenen linearen Systemen von Differentialgleichungen mit konstanten Koeffizienten nicht verschweigen.
Setzen wir
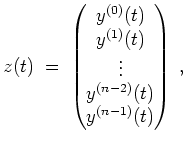
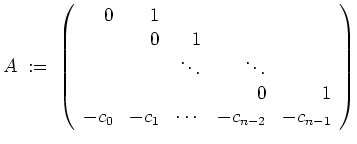
Das charakteristische Polynom der Matrix
![]() entspricht dabei dem zugehörigen charakteristischen Polynom der gegebenen
Differentialgleichung.
entspricht dabei dem zugehörigen charakteristischen Polynom der gegebenen
Differentialgleichung.
Analog kann man auch ein homogenes System
![]() -ter Ordnung mit
-ter Ordnung mit
![]() abhängigen Variablen
abhängigen Variablen
![]() , ...,
, ...,
![]() zurückführen auf ein homogenes System erster Ordnung mit
zurückführen auf ein homogenes System erster Ordnung mit
![]() abhängigen
Variablen.
abhängigen
Variablen.
Inhomogene lineare Differentialgleichungen
![]() -ter Ordnung mit konstanten Koeffizienten.
-ter Ordnung mit konstanten Koeffizienten.
Die allgemeine Lösung der inhomogenen linearen Differentialgleichung
![]() -ter Ordnung
mit konstanten Koeffizienten
-ter Ordnung
mit konstanten Koeffizienten
Nachdem im obigen Abschnitt beschrieben wird, wie man die allgemeine Lösung der homogenen Differentialgleichung
erhält, möchten wir uns auf die Bestimmung einer partikulären Lösung
![]() konzentrieren. Dabei möchten
wir drei Vorgehensweisen beschreiben.
konzentrieren. Dabei möchten
wir drei Vorgehensweisen beschreiben.
I. Ansatz vom Typ der rechten Seite.
Oftmals besitzt die Funktion
![]() , die in diesem Zusammenhang auch Störfunktion genannt wird,
eine einfache Gestalt, für die sich der Lösungsansatz zur Bestimmung der partikulären Lösung gemäß
der folgenden Tabelle ergibt.
, die in diesem Zusammenhang auch Störfunktion genannt wird,
eine einfache Gestalt, für die sich der Lösungsansatz zur Bestimmung der partikulären Lösung gemäß
der folgenden Tabelle ergibt.

Ist dabei
![]() bzw.
bzw.
![]() keine Nullstelle des zugehörigen charakteristischen Polynoms, so
wählen wir entsprechend
keine Nullstelle des zugehörigen charakteristischen Polynoms, so
wählen wir entsprechend
![]() . Liegen ferner Linearkombinationen solcher Störfunktionen vor, so wählt man
als Lösungsansatz für die partikuläre Lösung
. Liegen ferner Linearkombinationen solcher Störfunktionen vor, so wählt man
als Lösungsansatz für die partikuläre Lösung
![]() eine entsprechende Linearkombination der Ansatzfunktionen.
eine entsprechende Linearkombination der Ansatzfunktionen.
Man berechnet nun
II. Variation der Konstanten
Wir wählen den folgenden Ansatz zur Bestimmung einer partikulären Lösung
![]() der gegebenen Differentialgleichung.
der gegebenen Differentialgleichung.
Die Funktionen
![]() ermittelt man nun mittels der
ermittelt man nun mittels der
![]() Gleichungen
Gleichungen
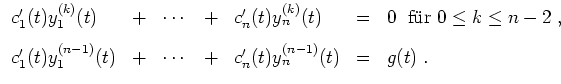
III. Zurückführung auf ein inhomogenes lineares System mit konstanten Koeffizienten.
Mit
![]() und
und
![]() wie im homogenen Fall und mit
wie im homogenen Fall und mit