Die Gleichung läßt sich umformen zu
Die Substitution
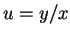 führt auf die Gleichung
Dies ist eine trennbare Gleichung. Es ergibt sich aus
daß
mit einer Konstanten
führt auf die Gleichung
Dies ist eine trennbare Gleichung. Es ergibt sich aus
daß
mit einer Konstanten
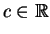 , und daher
mit einer Konstanten
, und daher
mit einer Konstanten
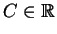 , und schließlich
, und schließlich
Das Richtungsfeld und die Lösung durch den Punkt
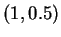 .
.
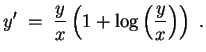
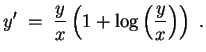
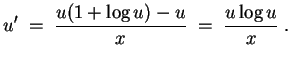
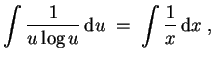
![]() .
.
![\includegraphics[width=10cm]{s2_homogen.eps}](img11.gif)