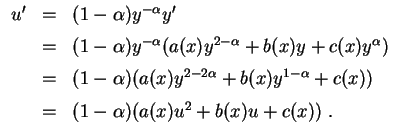
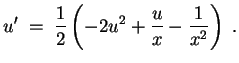
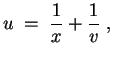
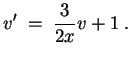
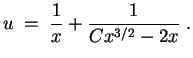
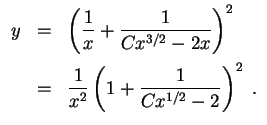
Ist zum Beispiel
![]() gewählt, so ergibt sich für
gewählt, so ergibt sich für
![]() folgende Lösung.
folgende Lösung.
![\includegraphics [width=10cm]{s1_u.eps}](img23.gif)
Für
![]() ist
ist
![]() eine Lösung der ursprünglichen Differentialgleichung.
eine Lösung der ursprünglichen Differentialgleichung.
![\includegraphics [width=10cm]{s1_valid_y.eps}](img26.gif)
Für
![]() ist
ist
![]() hingegen eine Lösung der Gleichung
hingegen eine Lösung der Gleichung
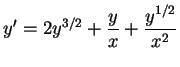 .
.
![\includegraphics[width=10cm]{s1_invalid_y.eps}](img29.gif)
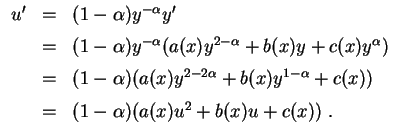
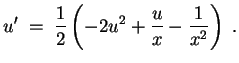
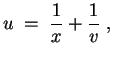
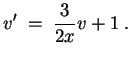
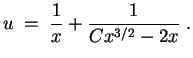
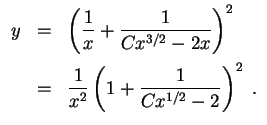
Ist zum Beispiel
![]() gewählt, so ergibt sich für
gewählt, so ergibt sich für
![]() folgende Lösung.
folgende Lösung.
![\includegraphics [width=10cm]{s1_u.eps}](img23.gif)
Für
![]() ist
ist
![]() eine Lösung der ursprünglichen Differentialgleichung.
eine Lösung der ursprünglichen Differentialgleichung.
![\includegraphics [width=10cm]{s1_valid_y.eps}](img26.gif)
Für
![]() ist
ist
![]() hingegen eine Lösung der Gleichung
hingegen eine Lösung der Gleichung
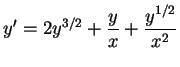 .
.
![\includegraphics[width=10cm]{s1_invalid_y.eps}](img29.gif)