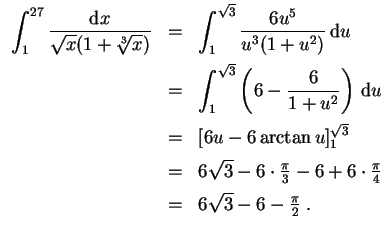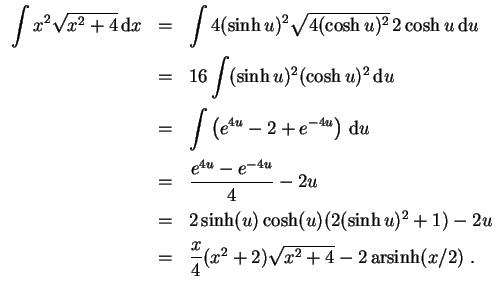- (1)
- Wir erhalten mit partieller Integration
und somit
- (2)
- Sei
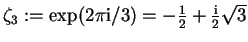 . Es ist
. Es ist
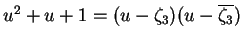 .
Mit der Substitution
.
Mit der Substitution
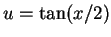 und Partialbruchzerlegung wird
und Partialbruchzerlegung wird
- (3)
- Es werden
- (4)
- Mit der Substitution
![$ \mbox{$u=\sqrt[6]{x}$}$](img8.gif) bzw.
bzw.
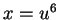 und
und
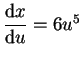 wird
wird
- (5)
- Wir wollen
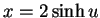 substitutieren. Wegen
substitutieren. Wegen
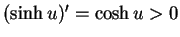 für alle
für alle
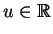 ist
ist
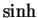 streng monton wachsend.
Da ferner
streng monton wachsend.
Da ferner
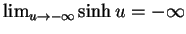 und
und
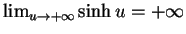 , besitzt
, besitzt
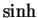 auf
auf
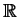 eine Umkehrfunktion,
den Area sinus hyperbolicus, geschrieben
eine Umkehrfunktion,
den Area sinus hyperbolicus, geschrieben
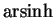 . Es wird
. Es wird
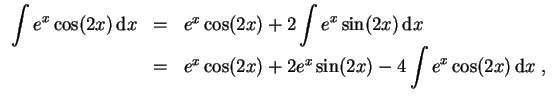
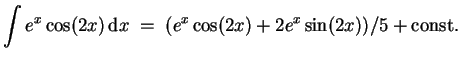
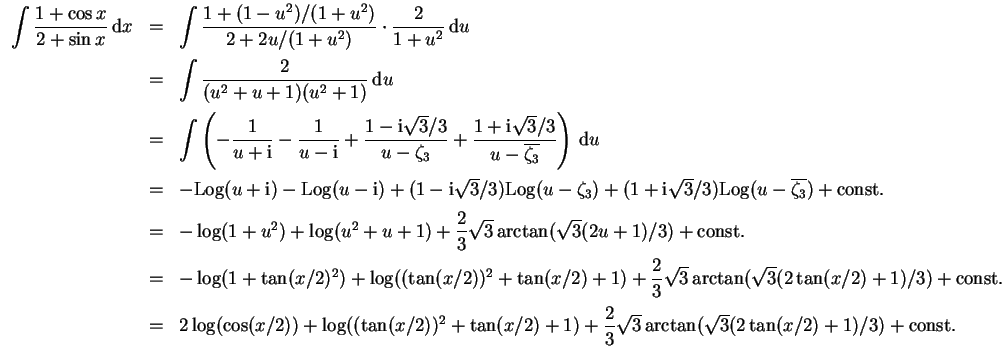
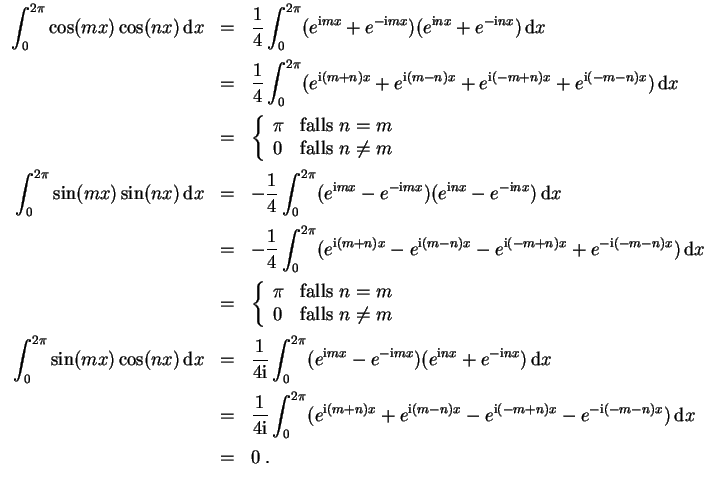
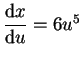 wird
wird
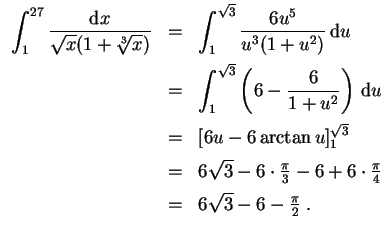
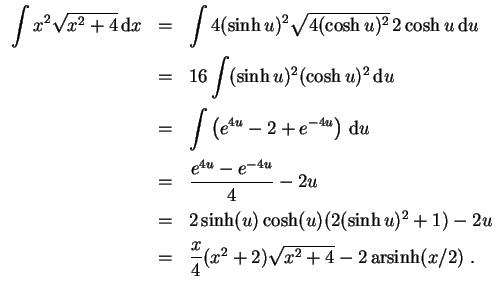
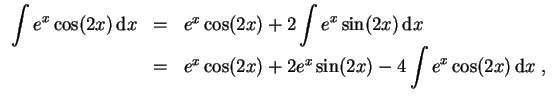
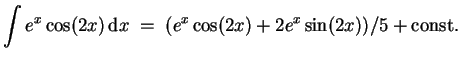
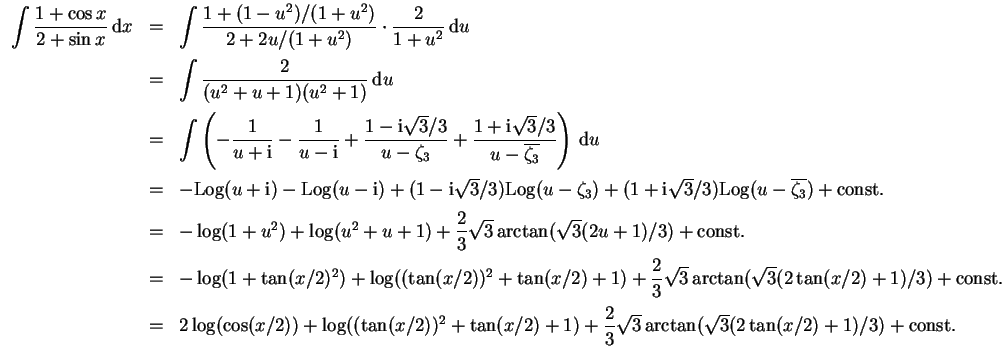
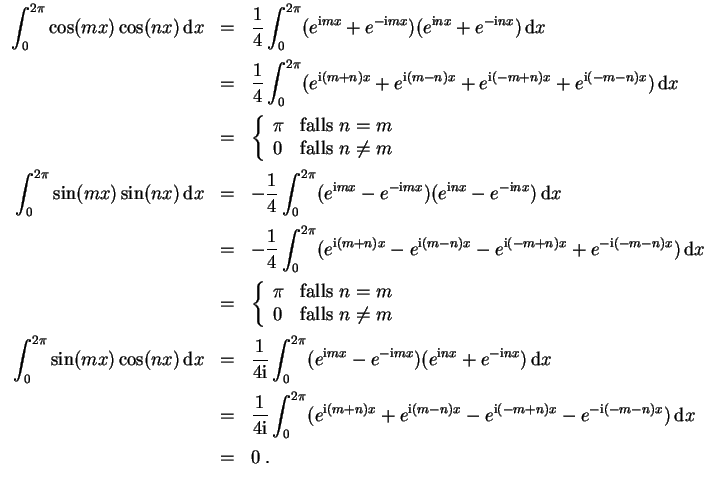
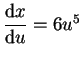 wird
wird