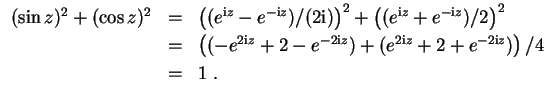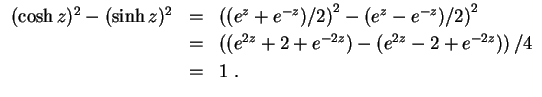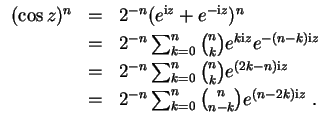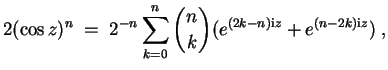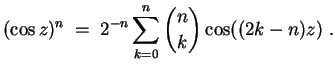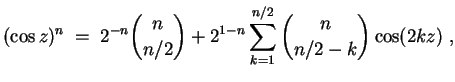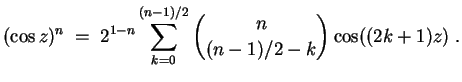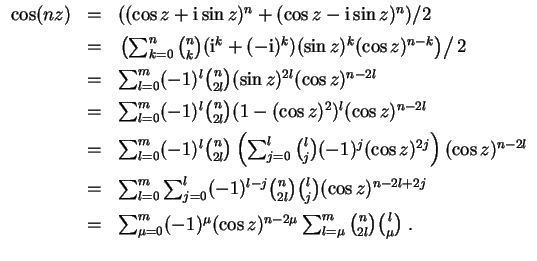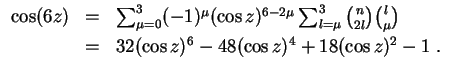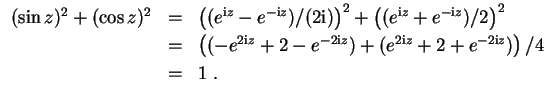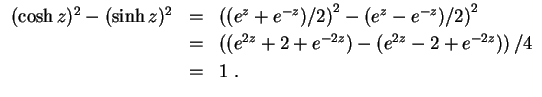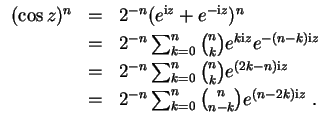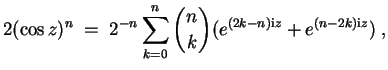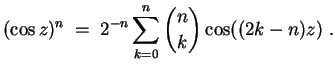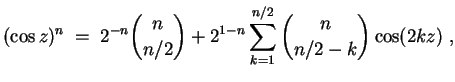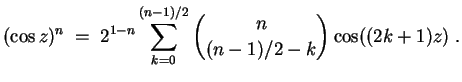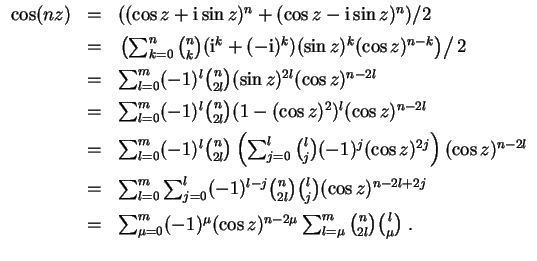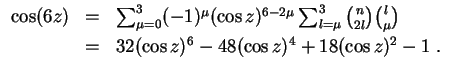- (1)
- Es wird
- (2)
- Es wird
- (3)
- Es wird
Unter Beachtung von
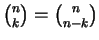 erhalten wir nach Summation der letzten beiden Ausdrücke
und somit
Irredundant geschrieben wird für
erhalten wir nach Summation der letzten beiden Ausdrücke
und somit
Irredundant geschrieben wird für
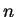 gerade also
und für
gerade also
und für
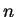 ungerade
ungerade
- (4,5)
- Sei
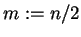 für
für
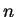 gerade und
gerade und
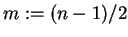 für
für
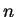 ungerade. Es wird
Insbesondere wird
Man kann hier auch auf direkten Wegen unter Verwendung des Additionstheorems zum Ziel gelangen.
ungerade. Es wird
Insbesondere wird
Man kann hier auch auf direkten Wegen unter Verwendung des Additionstheorems zum Ziel gelangen.