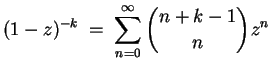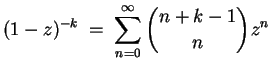Aufgabe.

Man überprüfe die Identität

$ \mbox{$\displaystyle (1-z)^{-k} \; = \; \sum_{n = 0}^\infty {n + k - 1 \choose n} z^n $}$
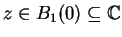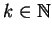für $ \mbox{$z\in B_1(0)\subseteq \mathbb{C}$}$ und $ \mbox{$k\in\mathbb{N}$}$.

(1)
Man verwende hierzu die Binomialreihe.
(2)
Man verwende hierzu Induktion über 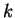$ \mbox{$k$}$, und das Cauchyprodukt für den Induktionsschritt.
(3)
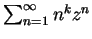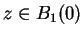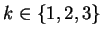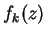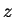Man berechne $ \mbox{$\sum_{n = 1}^\infty n^k z^n$}$ für $ \mbox{$z\in B_1(0)$}$ und $ \mbox{$k\in\{1,2,3\}$}$. Ergebnis jeweils als rationale Funktion $ \mbox{$f_k(z)$}$ in $ \mbox{$z$}$.
(4*)
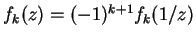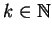$ \mbox{$f_k(z) = (-1)^{k+1} f_k(1/z)$}$ für alle $ \mbox{$k\in\mathbb{N}$}$.