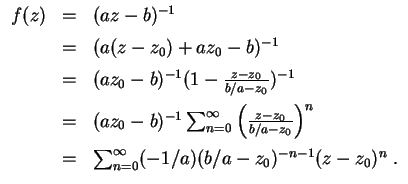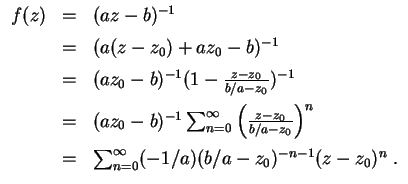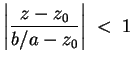Lösung.

Wir formen so um, daß die geometrische Reihenentwicklung verwandt werden kann, namentlich

$ \mbox{$\displaystyle \begin{array}{rcl} f(z) & = & (az - b)^{-1} \vspace*{2mm... ...& \sum_{n = 0}^\infty (-1/a)(b/a - z_0)^{-n-1} (z-z_0)^n \; .\\ \end{array}$}$
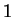Zur Bestimmung des Konvergenzradius kann man nun die Cauchy-Hadamardsche Formel auf die Koeffizienten anwenden. Alternativ kann man aber auch verwenden, daß die geometrische Reihe den Konvergenzradius $ \mbox{$1$}$ hat, und unsere Reihe folglich genau für
$ \mbox{$\displaystyle \left\vert\frac{z-z_0}{b/a - z_0}\right\vert \; <\; 1 $}$
konvergiert. Der Konvergenzradius ergibt sich somit zu
$ \mbox{$\displaystyle R\; =\; \vert b/a - z_0\vert\; . $}$
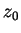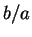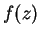Dies ist gerade der Abstand vom Entwicklungspunkt $ \mbox{$z_0$}$ zur Polstelle $ \mbox{$b/a$}$ von $ \mbox{$f(z)$}$.