Es sei
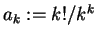 .
.
- Es wird
Also ist
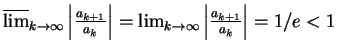 , und die Reihe konvergiert absolut nach dem Quotientenkriterium.
, und die Reihe konvergiert absolut nach dem Quotientenkriterium.
- Es wird
nach der schwachen Form der Stirlingschen Formel.
Also ist
![$ \mbox{$\overline {\lim}_{k\to\infty}\sqrt[k]{\vert a_k\vert}=1/e<1$}$](img5.gif) , und die Reihe konvergiert absolut nach dem Wurzelkriterium.
, und die Reihe konvergiert absolut nach dem Wurzelkriterium.
![]() .
.
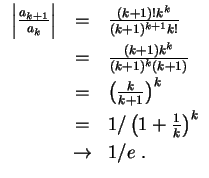
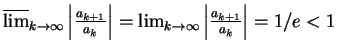 , und die Reihe konvergiert absolut nach dem Quotientenkriterium.
, und die Reihe konvergiert absolut nach dem Quotientenkriterium.
![$ \mbox{$\displaystyle
\sqrt[k]{\vert a_k\vert} \;=\; \frac{\sqrt[k]{k!}}{k} \;\to\; 1/e
$}$](img4.gif)