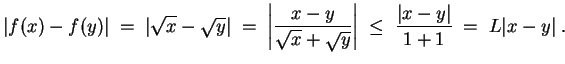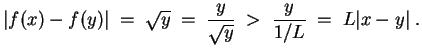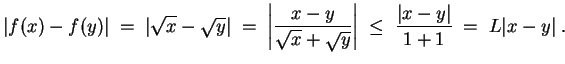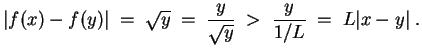Nach 1. und 2. ist
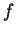 gleichmäßig stetig auf
gleichmäßig stetig auf
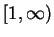 .
Ferner ist
.
Ferner ist
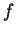 stetig auf
stetig auf
![$ \mbox{$[0,1]$}$](img10.gif) , und
, und
![$ \mbox{$[0,1]$}$](img10.gif) ist kompakt. Daher ist
ist kompakt. Daher ist
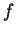 auch gleichmäßig stetig auf
auch gleichmäßig stetig auf
![$ \mbox{$[0,1]$}$](img10.gif) . Wir zeigen nun damit die gleichmäßige Stetigkeit von
. Wir zeigen nun damit die gleichmäßige Stetigkeit von
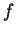 auf der Menge
auf der Menge
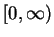 .
Es sei
.
Es sei
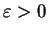 vorgegeben. Dann gibt es also
vorgegeben. Dann gibt es also
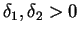 so, daß
für alle
so, daß
für alle
![$ \mbox{$x_1,x_2\in[0,1]$}$](img23.gif) mit
mit
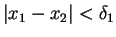 und alle
und alle
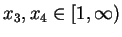 mit
mit
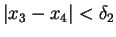 .
Wir setzen
.
Wir setzen
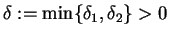 . Seien nun
. Seien nun
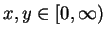 mit
mit
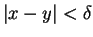 , und ohne
Einschränkung sei
, und ohne
Einschränkung sei
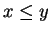 .
In den Fällen
.
In den Fällen
![$ \mbox{$x,y\in[0,1]$}$](img13.gif) oder
oder
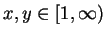 folgt dann sofort
folgt dann sofort
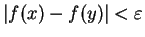 .
Im Fall
.
Im Fall
![$ \mbox{$x\in[0,1],y\in[1,\infty)$}$](img31.gif) gilt auch
gilt auch
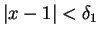 und
und
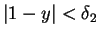 , und somit wird
Damit ist die gleichmäßige Stetigkeit von
, und somit wird
Damit ist die gleichmäßige Stetigkeit von
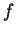 auf
auf
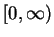 gezeigt.
gezeigt.
Vorsicht, das entsprechende Argument versagt, wenn man statt zweier vielmehr unendlich viele Intervalle zusammensetzen
möchte.