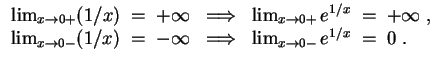
Es gilt
![]() und
und
![]() .
Daraus folgt
.
Daraus folgt
![]() .
.
Wäre die komplexe Funktion
![]() konvergent für
konvergent für
![]() , so wäre wegen
, so wäre wegen
![]() auch die Folge
auch die Folge
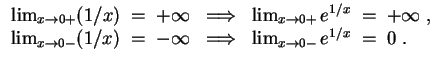
Es gilt
![]() und
und
![]() .
Daraus folgt
.
Daraus folgt
![]() .
.
Wäre die komplexe Funktion
![]() konvergent für
konvergent für
![]() , so wäre wegen
, so wäre wegen
![]() auch die Folge
auch die Folge