- Es wird
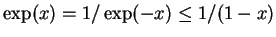 für
für
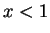 . Daraus ergibt sich
sofern
. Daraus ergibt sich
sofern
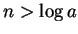 . Mit
. Mit
![$ \mbox{$\sqrt[n]{a}=\exp(\log(a)/n)$}$](img5.gif) und dem Vergleichskriterium folgt
und dem Vergleichskriterium folgt
![$ \mbox{$\sqrt[n]{a}\to 1$}$](img6.gif) für
für
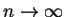 .
.
- Mit
bleibt uns für
![$ \mbox{$\sqrt[n]{n} = \exp(\log(n)/n) \to 1$}$](img9.gif) für
für
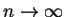 mit dem Vergleichskriterium zu zeigen, daß
mit dem Vergleichskriterium zu zeigen, daß
 .
.
Es wird aber
für
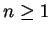 , denn es gilt allgemein
, denn es gilt allgemein
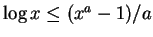 für
für
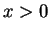 und
und
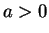 . Die Aussage folgt nun
mit dem Vergleichskriterium.
. Die Aussage folgt nun
mit dem Vergleichskriterium.
- Die Aussage trifft zu für
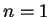 . Sei die Aussage für
. Sei die Aussage für
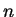 als richtig angenommen und für
als richtig angenommen und für
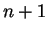 zu zeigen.
Wir erhalten
zu zeigen.
Wir erhalten
- Aus (3) folgt nach Potenzieren mit
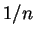 und nach Division durch
und nach Division durch
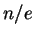 und die Aussage folgt mit (1,2) und dem Vergleichskriterium.
und die Aussage folgt mit (1,2) und dem Vergleichskriterium.
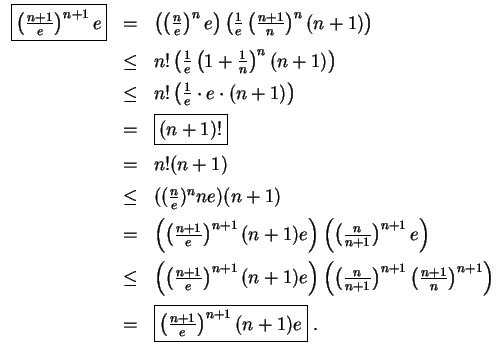
![$ \mbox{$\displaystyle
\sqrt[n]{e}\;\leq\; \frac{\sqrt[n]{n!}}{n/e} \;\leq\; \sqrt[n]{ne}\; ,
$}$](img22.gif)
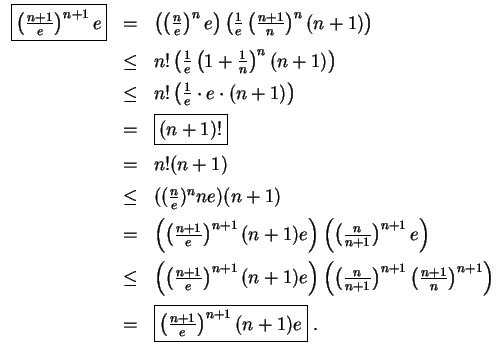
![$ \mbox{$\displaystyle
\sqrt[n]{e}\;\leq\; \frac{\sqrt[n]{n!}}{n/e} \;\leq\; \sqrt[n]{ne}\; ,
$}$](img22.gif)