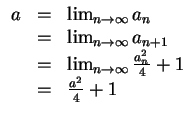Wir zeigen zunächst unabhängig vom Wert
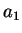 die wachsende Monotonie der Folge. Es wird
die wachsende Monotonie der Folge. Es wird
- (i)
- Wir zeigen die Beschränktheit der Folge, indem wir per Induktion die Aussage
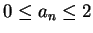 zeigen.
Für
zeigen.
Für
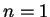 ist dies klar. Sei nun
ist dies klar. Sei nun
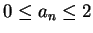 gegeben, und
gegeben, und
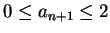 zu zeigen.
In der Tat wird
zu zeigen.
In der Tat wird
Nach dem Monotoniekriterium konvergiert die Folge
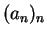 also gegen einen Grenzwert
also gegen einen Grenzwert
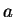 .
Wir behaupten
.
Wir behaupten
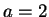 .
Aus
.
Aus
folgt
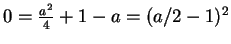 , also
, also
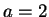 .
.
- (ii)
- Aus der Monotonie der Folge erhalten wir
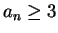 für alle
für alle
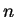 , und somit
Daher ist die Folge nicht nach oben beschränkt. Da sie monoton wächst, divergiert sie bestimmt gegen
, und somit
Daher ist die Folge nicht nach oben beschränkt. Da sie monoton wächst, divergiert sie bestimmt gegen
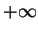 .
.
![]() die wachsende Monotonie der Folge. Es wird
die wachsende Monotonie der Folge. Es wird
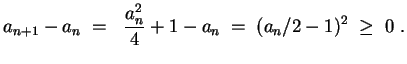
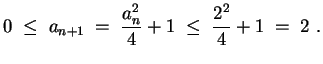
![]() also gegen einen Grenzwert
also gegen einen Grenzwert
![]() .
Wir behaupten
.
Wir behaupten
![]() .
Aus
.
Aus