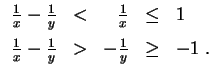
Zunächst ist stets
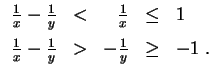
Wir behaupten, daß
![]() . Dies ist eine obere Schranke, und es bleibt zu zeigen, daß
. Dies ist eine obere Schranke, und es bleibt zu zeigen, daß
![]() keine
obere Schranke mehr ist. Da
keine
obere Schranke mehr ist. Da
![]() , dürfen wir
, dürfen wir
![]() annehmen.
Für
annehmen.
Für
![]() wählen wir
wählen wir
![]() (ist
(ist
![]() !) und
!) und
![]() (ist ebenfalls
(ist ebenfalls
![]() !) und erhalten
!) und erhalten
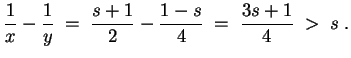
Zum Beweis von
![]() merken wir an, daß
merken wir an, daß
![]() genau dann eine obere Schranke von
genau dann eine obere Schranke von
![]() ist, wenn
ist, wenn
![]() eine untere Schranke von
eine untere Schranke von
![]() ist. Aus
ist. Aus
![]() folgt, daß
folgt, daß
![]() kein Minimum besitzt.
kein Minimum besitzt.