Ist
![]() mit
mit
![]() , so ist
, so ist
![]() genau dann,
wenn
genau dann,
wenn
![]() , d.h. wenn
, d.h. wenn
![]() ist, d.h.
ist, d.h.
![]() .
.
Ferner ist
![]() genau dann,
wenn
genau dann,
wenn
![]() , d.h. wenn
, d.h. wenn
![]() ist, d.h.
ist, d.h.
![]() .
.
Um den genannten Ausdruck als reell nachzuweisen, berechnen wir sein Konjugiertes. Es wird
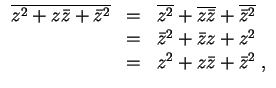
Schließlich werden
![]() und
und
![]() .
.