Approximation Numbers of Sobolev Embeddings

Let $ W^k_p$ denote the Sobolev space of $ k$-times differentiable functions $ f$ in $ L_p$ on a bounded Lipschitz domain $ D$ in $ \mathbb{R}^d$. If $ k>d$ and $ 1\le p < 2 < q\le\infty$,

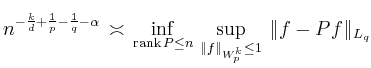
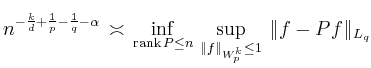
$\displaystyle n^{-\frac{k}{d}+\frac{1}{p}-\frac{1}{q}-\alpha} \,\asymp\, \inf... ...ank}P\le n}\, \sup_{\Vert f\Vert _{W^k_p}\le 1}\, \Vert f - P f\Vert _{L_q} $

with $ \alpha = \min(1/2-1/q,1/p-1/2)$ and the symbol $ \asymp$ indicating inequalities in both directions with constants not depending on $ n\in\mathbb{N}$.

Asymptotically optimal approximation operators $ P$ improve the exponent for standard schemes, such as spline interpolants or finite element projections, by $ \alpha$. The gain is maximal for $ p=1$, $ q=\infty$, when $ \alpha=1/2$.

\includegraphics[width=10cm]{ApproximationFig.eps}

The figure shows the exponents for all values of $ p,p\in[1,\infty]$. Apparently, classical methods are optimal for $ p\ge 2$ and $ q\le 2$ (white area).


$ \square$ Dissertation, Bonn, 1979

$ \square$ Math. Annalen, 242 (1979), 273-281

[previous] [next]